The volume V of a liquid crossing through a tube is related to the area of cross-section A, velocity v and time t as VαAavbtc which of the following is correct ( given a≠1 )
a≠b≠c
a=b=c
a≠b=c
a=b≠c
The correct Answer is:C
To solve the problem, we need to analyze the relationship given in the question using dimensional analysis. The relationship is given as:
V∝Aavbtc
Where:
- V is the volume,
- A is the area of cross-section,
- v is the velocity,
- t is the time,
- a,b,c are the exponents we need to determine.
Step 1: Write down the dimensions of each quantity.
- The dimension of volume V is (V)=L3 (length cubed).
- The dimension of area A is (A)=L2 (length squared).
- The dimension of velocity v is (v)=LT−1 (length per time).
- The dimension of time t is (t)=T (time).
Step 2: Write the dimensional equation based on the given relationship.
Using the dimensions, we can express the relationship dimensionally:
L3=(L2)a⋅(LT−1)b⋅(T)c
Step 3: Simplify the right side of the equation.
Now, simplifying the right side:
L3=L2a⋅Lb⋅T−b⋅Tc
Combining the dimensions gives:
L3=L2a+b⋅Tc−b
Step 4: Equate the dimensions on both sides.
For the equation to hold true, the dimensions on both sides must be equal. This gives us two equations:
1. For length:
2a+b=3
2. For time:
c−b=0⇒c=b
Step 5: Substitute c into the first equation.
Since c=b, we can substitute b into the first equation:
2a+b=3
Now, we can express a in terms of b:
2a=3−b⇒a=3−b2
Step 6: Analyze the relationships between a,b,c.
From the equations we have:
- c=b
- a=3−b2
Given that a≠1, we can analyze the relationships:
- If b=0, then a=3−02=1.5 and c=0.
- If b≠0, then a will not equal b because a will always be 3−b2.
Conclusion: Identify the correct option.
From the analysis, we find that:
- a is not equal to b (since a=3−b2),
- b is equal to c.
Thus, the correct option is:
Option 3: A is not equal to B and B is equal to C.
- V is the volume,
- A is the area of cross-section,
- v is the velocity,
- t is the time,
- a,b,c are the exponents we need to determine.
- The dimension of area A is (A)=L2 (length squared).
- The dimension of velocity v is (v)=LT−1 (length per time).
- The dimension of time t is (t)=T (time).
2a+b=3
c−b=0⇒c=b
- c=b
- a=3−b2
- If b=0, then a=3−02=1.5 and c=0.
- If b≠0, then a will not equal b because a will always be 3−b2.
- a is not equal to b (since a=3−b2),
- b is equal to c.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE - I
156 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
Similar Questions
Knowledge Check
In the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities vA and vB, and pressures PA and PB at the points A and B, respectively. Then
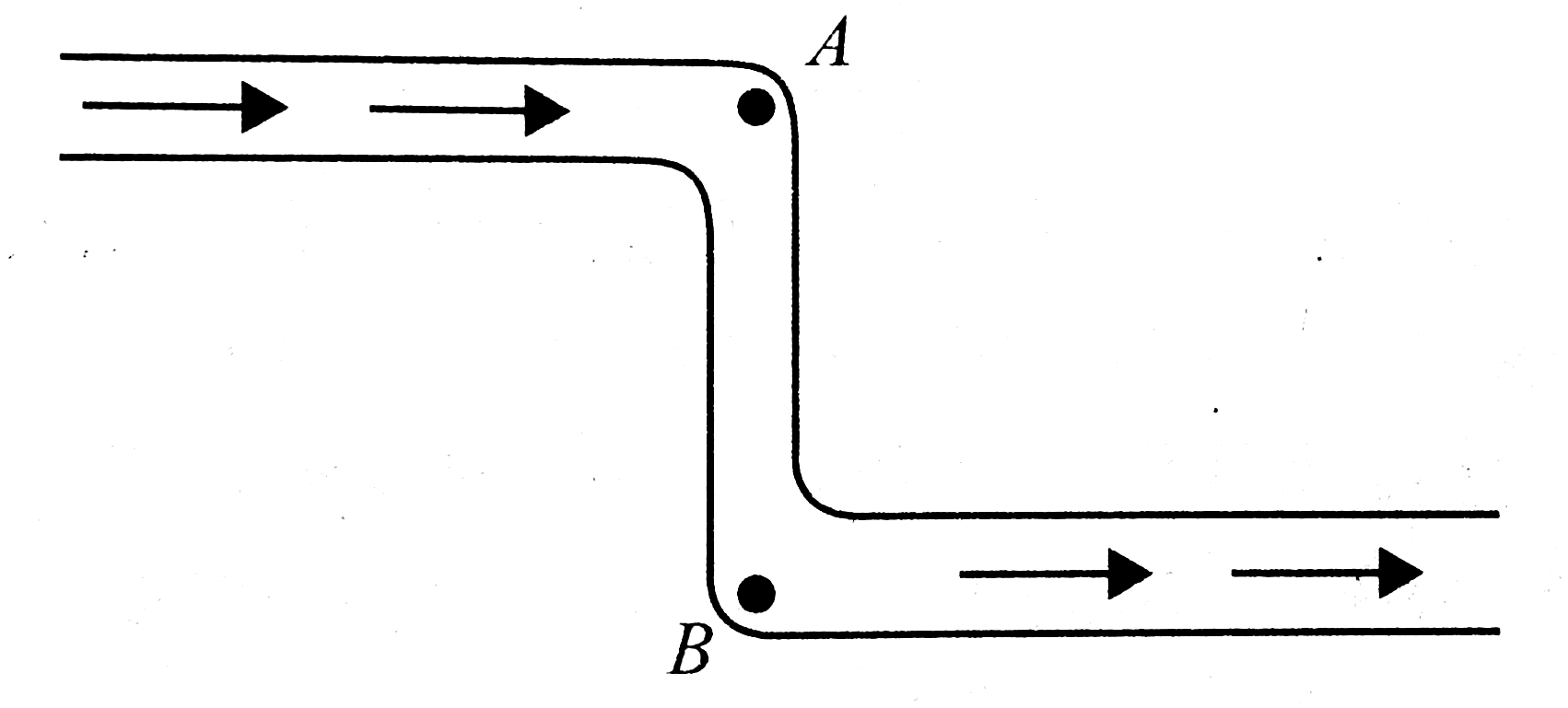 AvB>vABvB=vACPB<PADPB=PA
AvB>vABvB=vACPB<PADPB=PA
If velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View SolutionThe value of drift speeds at cross section (1) and (2) are V1 and V2 respectively in the conductor shown below in the shape of a truncated cone .
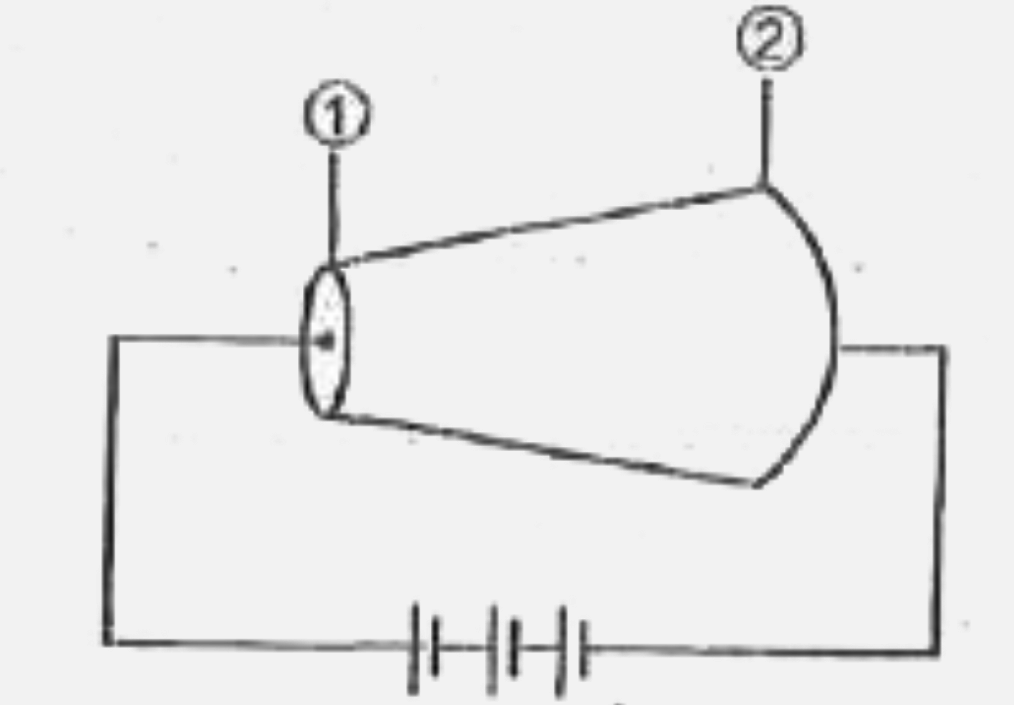
Which of the following is correct ?
View SolutionThe mass of the liquid flowing per second per unit area of cross-section of the tube is proportional to (pressure difference across the ends)^(n) and (average velocity of the liquid)^(m) . Which of the following relations between m and n is correct?
View SolutionCurrent 'I' flowing through a metallic wire of area of cross-section 'a' is given by the equation I=naevd. What is the meaning of the symbols 'n' and 'vd'?
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
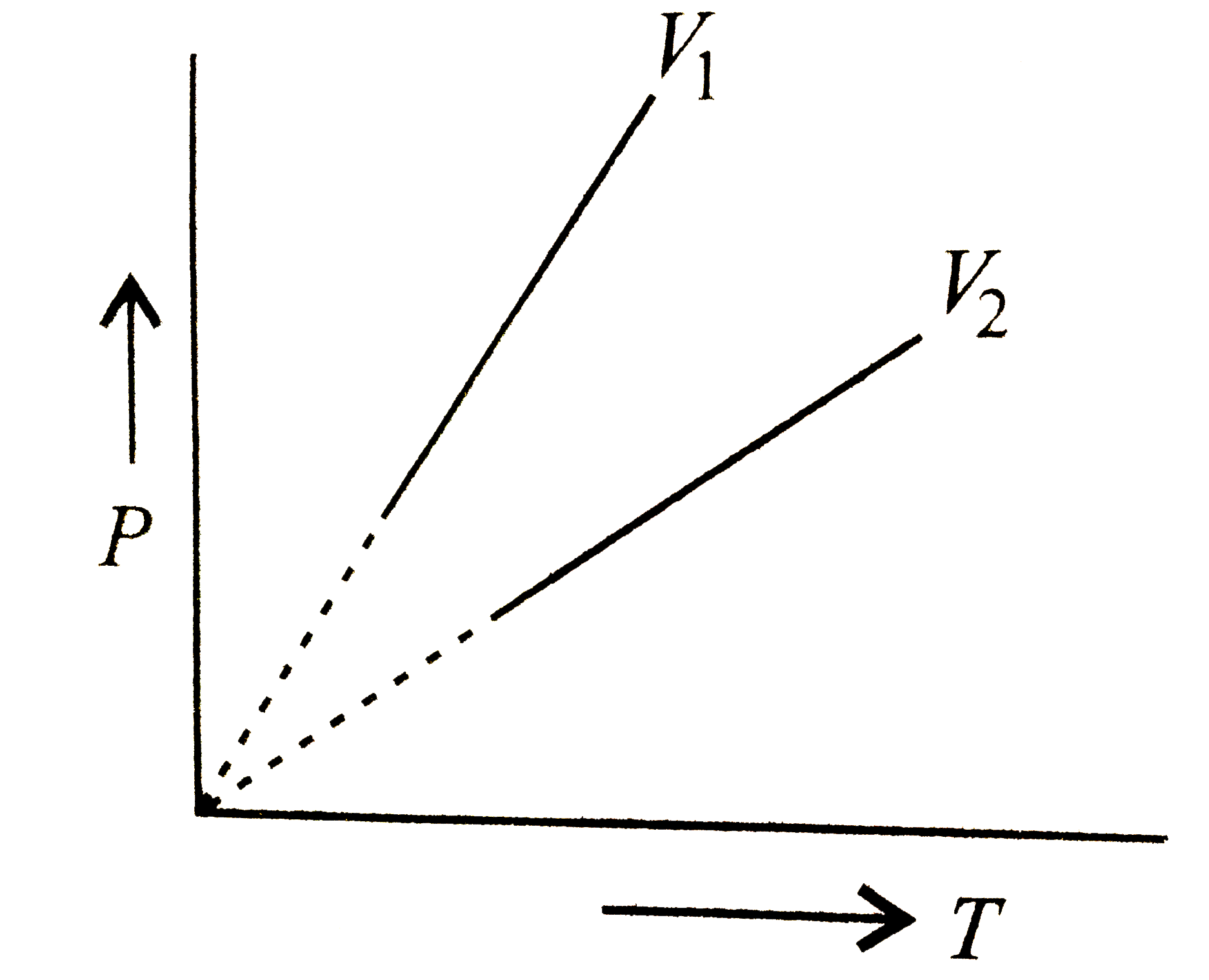
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View Solution
