A man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37° with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
1ms−1
2ms−1
3ms−1
4ms−1
The correct Answer is:D
To solve the problem, we need to determine the velocity of the rain (V_rain) given the velocity of the car (V_car) and the angle at which the umbrella is held (θ). Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
The car is moving horizontally at a speed of 10.8 km/h, and the rain is falling vertically downwards. The umbrella is held at an angle of 37° with the vertical to prevent the man from getting wet.
Step 2: Convert the Speed of the Car
Convert the speed of the car from km/h to m/s for consistency in units.
Vcar=10.8 km/h=10.8×1000 m3600 s=3 m/s
Step 3: Draw a Diagram
Visualize the situation:
- The velocity of the car (V_car) is horizontal.
- The velocity of the rain (V_rain) is vertical.
- The umbrella makes an angle of 37° with the vertical.
Step 4: Determine the Angles
Since the umbrella is at an angle of 37° with the vertical, the angle with the horizontal (θ) is:
θ=90°−37°=53°
Step 5: Use Trigonometry
Using the tangent function, which relates the opposite side (V_rain) to the adjacent side (V_car):
tan(θ)=VrainVcar
Substituting the known values:
tan(53°)=Vrain3 m/s
Step 6: Calculate the Tangent
Calculate the value of tan(53°):
tan(53°)≈1.327
Step 7: Solve for V_rain
Now, substituting this value into the equation:
1.327=Vrain3
Thus,
Vrain=1.327×3 m/s≈3.981 m/s
Step 8: Round the Result
Rounding this to a more manageable figure, we can say:
Vrain≈4 m/s
Final Answer
The velocity of the rain is approximately 4 m/s.
---
The car is moving horizontally at a speed of 10.8 km/h, and the rain is falling vertically downwards. The umbrella is held at an angle of 37° with the vertical to prevent the man from getting wet.
Convert the speed of the car from km/h to m/s for consistency in units.
Vcar=10.8 km/h=10.8×1000 m3600 s=3 m/s
Visualize the situation:
- The velocity of the car (V_car) is horizontal.
- The velocity of the rain (V_rain) is vertical.
- The umbrella makes an angle of 37° with the vertical.
Since the umbrella is at an angle of 37° with the vertical, the angle with the horizontal (θ) is:
θ=90°−37°=53°
Using the tangent function, which relates the opposite side (V_rain) to the adjacent side (V_car):
tan(θ)=VrainVcar
Substituting the known values:
tan(53°)=Vrain3 m/s
Calculate the value of tan(53°):
tan(53°)≈1.327
Now, substituting this value into the equation:
1.327=Vrain3
Thus,
Vrain=1.327×3 m/s≈3.981 m/s
Rounding this to a more manageable figure, we can say:
Vrain≈4 m/s
The velocity of the rain is approximately 4 m/s.
Similar Questions
A man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical to protect himself from rain which is falling vertically downwards. What is the velocity of the rain drop ?
View SolutionA glass wind screen whose inclination with the vertical can be changed is mounted on a car. The moves horizontally with a speed of 2m/s. At what angle α with the vertical should the wind screen placed so that the rain drops falling vertically downwards with velcoity 6m/s strike the wind screen perpendicularly?
View SolutionWhen a man moves down the inclined plane with a constant speed 5ms−1 which makes an angle of 37∘ with the horizontal, he finds that the rain is falling vertically downward. When he moves up the same inclined plane with the same speed, he finds that the rain makes an angle θ=tan−1(78) with the horizontal. The speed of the rain is
View SolutionThere are two incline planes AO and OB inclined at 45∘ and 60∘ respectively with the horizontal as shown in the figure. When a man moves on the inclined plane AO he is oberves that the rain drops are falling 45∘ with the vertical. When the man moves on the inclined plane OB, he observes that the raindrops are falling vertically downward with the horizontal. Then actual speed of rain is
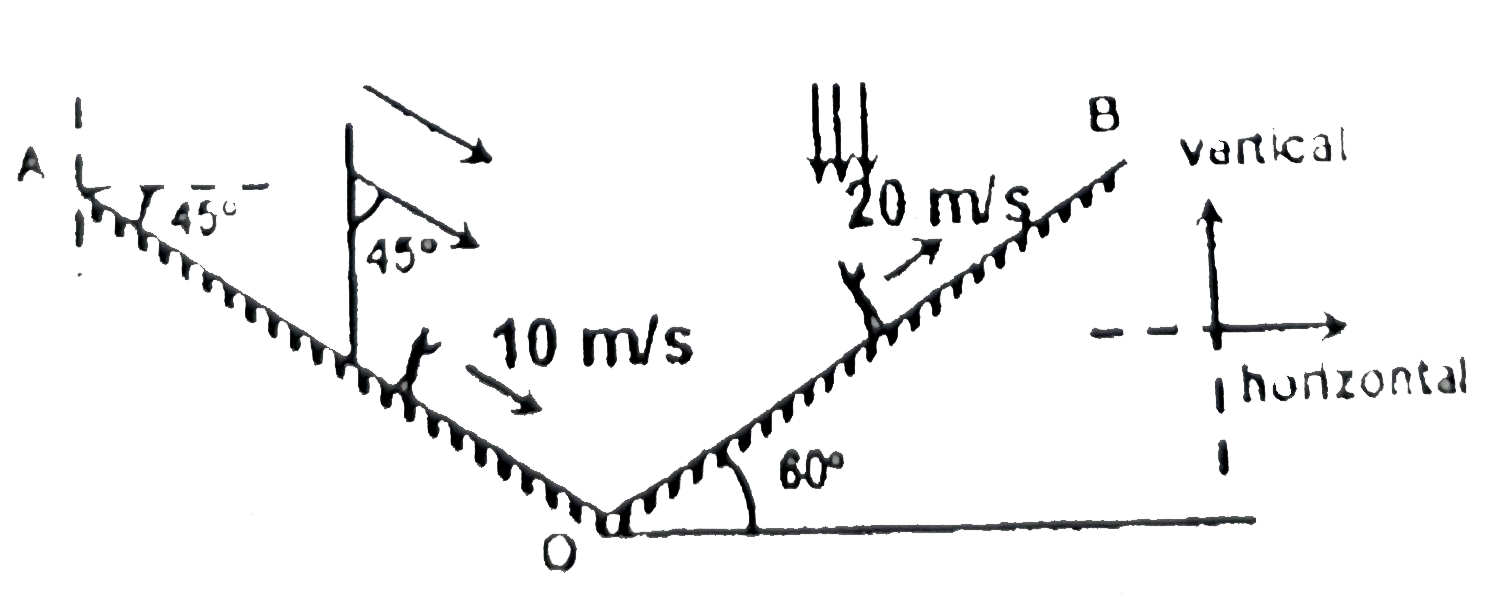
View SolutionA man runs along a horizontal road on a rainy day. His umbrella vertical in order to protect himself from the rain then rain actually
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionA man moving with a velocity of 5m/s on a horizontal road observes that raindrops fall at an angle of 45∘ with the vertical. When he moves with a velocity of 16m/s along an inclined plane, which is inclined at 30∘ with the horizontal , he observes raindrops falling vertically downward as shown in the figure. Find the actual velocity of the raindrops.
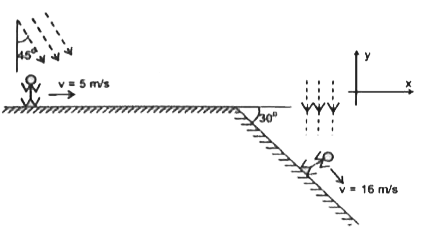
View SolutionA person is walking in rain feels the velocity of rain as twice to his velocity. At which angle he should hold the umbrella with vertical if he moves forward, if it is raining vertically downwards
View SolutionStatement -1 : A man standing on the ground has to hold his umbrella at an angle θ with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle θ with the vertical to protect himself from rain.
Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.
View Solution
