A person is walking in rain feels the velocity of rain as twice to his velocity. At which angle he should hold the umbrella with vertical if he moves forward, if it is raining vertically downwards
30∘
45∘
60∘
90∘
The correct Answer is:A
To solve the problem step by step, we will analyze the situation using vector components and trigonometric relationships.
Step 1: Understand the scenario
- The person is walking forward with a velocity vm.
- The rain is falling vertically downwards with a velocity vr.
- The person perceives the velocity of the rain as twice his own walking speed, i.e., vrm=2vm.
Step 2: Set up the coordinate system
- Let's define the horizontal direction (forward movement of the person) as the x-axis and the vertical direction (downward rain) as the y-axis.
- The velocity of the man can be represented as a vector: →vm=vm^i (where ^i is the unit vector in the x-direction).
- The velocity of the rain can be represented as: →vr=−vr^j (where ^j is the unit vector in the y-direction).
Step 3: Determine the relative velocity of the rain
- The relative velocity of the rain with respect to the man is given by:
→vrm=→vr−→vm=−vr^j−vm^i
- The magnitude of this relative velocity is given as vrm=2vm.
Step 4: Apply the Pythagorean theorem
- The magnitude of the relative velocity can be expressed as:
vrm=√(vm)2+(vr)2
- Setting this equal to 2vm:
√(vm)2+(vr)2=2vm
- Squaring both sides gives:
(vm)2+(vr)2=4(vm)2
- Rearranging leads to:
(vr)2=3(vm)2
- Therefore, we find:
vr=√3vm
Step 5: Find the angle at which to hold the umbrella
- The angle θ at which the umbrella should be held can be found using the sine function:
sinθ=vmvrm=vm2vm=12
- Thus, we find:
θ=sin−1(12)=30∘
Conclusion
- The person should hold the umbrella at an angle of 30∘ with respect to the vertical.
- The person is walking forward with a velocity vm.
- The rain is falling vertically downwards with a velocity vr.
- The person perceives the velocity of the rain as twice his own walking speed, i.e., vrm=2vm.
- Let's define the horizontal direction (forward movement of the person) as the x-axis and the vertical direction (downward rain) as the y-axis.
- The velocity of the man can be represented as a vector: →vm=vm^i (where ^i is the unit vector in the x-direction).
- The velocity of the rain can be represented as: →vr=−vr^j (where ^j is the unit vector in the y-direction).
- The relative velocity of the rain with respect to the man is given by:
→vrm=→vr−→vm=−vr^j−vm^i
- The magnitude of this relative velocity is given as vrm=2vm.
- The magnitude of the relative velocity can be expressed as:
vrm=√(vm)2+(vr)2
- Setting this equal to 2vm:
√(vm)2+(vr)2=2vm
- Squaring both sides gives:
(vm)2+(vr)2=4(vm)2
- Rearranging leads to:
(vr)2=3(vm)2
- Therefore, we find:
vr=√3vm
- The angle θ at which the umbrella should be held can be found using the sine function:
sinθ=vmvrm=vm2vm=12
- Thus, we find:
θ=sin−1(12)=30∘
- The person should hold the umbrella at an angle of 30∘ with respect to the vertical.
Similar Questions
When it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at an angle θ to vertical. Then tanθ=
View SolutionA boy is running on a horizontal road with a velocity of 5 m/s. At what angle should he hold his umbrella in order to protect him self from the rain if the rain is falling vertically with a velocity of 10 m/s?
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical to protect himself from rain which is falling vertically downwards. What is the velocity of the rain drop ?
View SolutionRain is falling vertically with velocity 10m /s and a man is moving with velocity 6ms−1. Find the angle at which the man should hold his umbrella to above getting wet.
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37° with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
View SolutionA glass wind screen whose inclination with the vertical can be changed is mounted on a car. The moves horizontally with a speed of 2m/s. At what angle α with the vertical should the wind screen placed so that the rain drops falling vertically downwards with velcoity 6m/s strike the wind screen perpendicularly?
View SolutionDuring a rainy day, rain is falling vertically with a velocity 2m/s A boy at rest starts his motion with a constant acceleration of 2m/s2 along a straight road . Find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain always falls parallel to the axis of the umbrella.
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
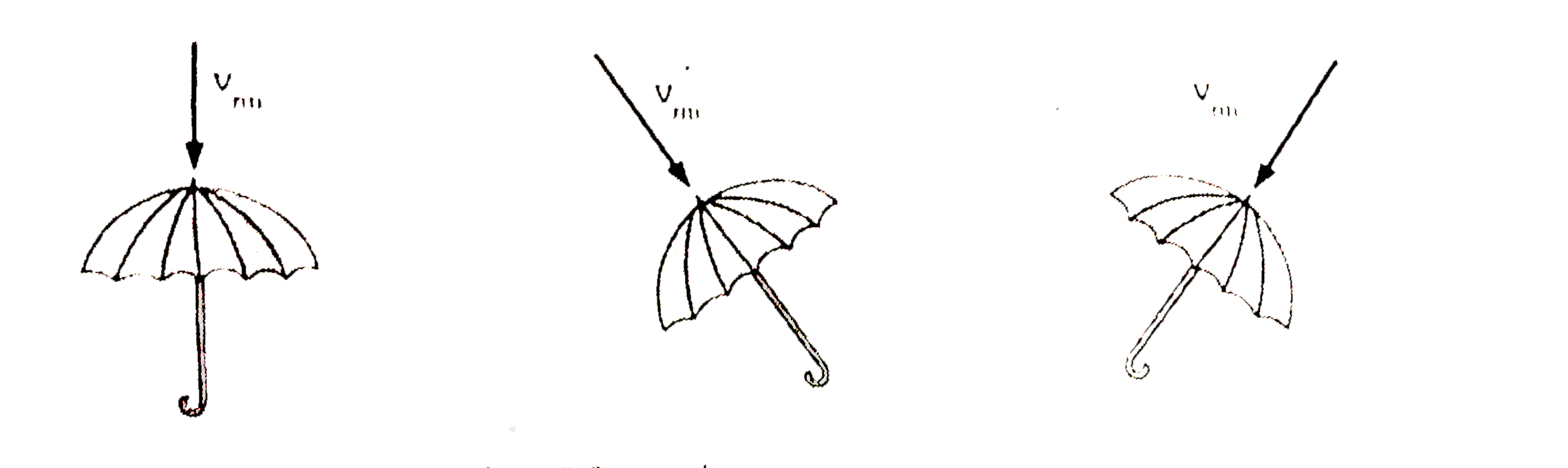
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.
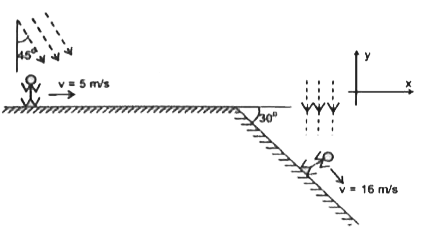
View SolutionA man moving with a velocity of 5m/s on a horizontal road observes that raindrops fall at an angle of 45∘ with the vertical. When he moves with a velocity of 16m/s along an inclined plane, which is inclined at 30∘ with the horizontal , he observes raindrops falling vertically downward as shown in the figure. Find the actual velocity of the raindrops.
View Solution
