The velocity of water in a river is 2 kmph, while width is 400 m. A boat is rowed from a point rowing always aiming opposite point at 8 kmph of still water velocity. On reaching the opposite bank the drift obtained is
93 m
100.8 m
112.4 m
100 m
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Convert the velocities from km/h to m/s
1. Velocity of water (u):
- Given: 2 km/h
- Conversion: u=2×518=1018=59 m/s
2. Velocity of the boat (v):
- Given: 8 km/h
- Conversion: v=8×518=4018=209 m/s
Step 2: Calculate the time taken to cross the river
- Width of the river (d): 400 m
- Time (t) to cross the river can be calculated using the formula:
t=dv=400209=400×920=180 seconds
Step 3: Calculate the drift
- The drift (x) is caused by the velocity of the water acting over the time taken to cross the river.
- Using the formula for drift:
x=u×t=59×180
- Calculating:
x=5×1809=100 meters
Final Answer
The drift obtained when the boat reaches the opposite bank is 100 meters.
---
1. Velocity of water (u):
- Given: 2 km/h
- Conversion: u=2×518=1018=59 m/s
- Given: 8 km/h
- Conversion: v=8×518=4018=209 m/s
- Width of the river (d): 400 m
- Time (t) to cross the river can be calculated using the formula:
t=dv=400209=400×920=180 seconds
- The drift (x) is caused by the velocity of the water acting over the time taken to cross the river.
- Using the formula for drift:
x=u×t=59×180
- Calculating:
x=5×1809=100 meters
The drift obtained when the boat reaches the opposite bank is 100 meters.
Similar Questions
A ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionA person swims at 135° to current of river, to meet target on reaching opposite point. The ratio of person's velocity to river water velocity is
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
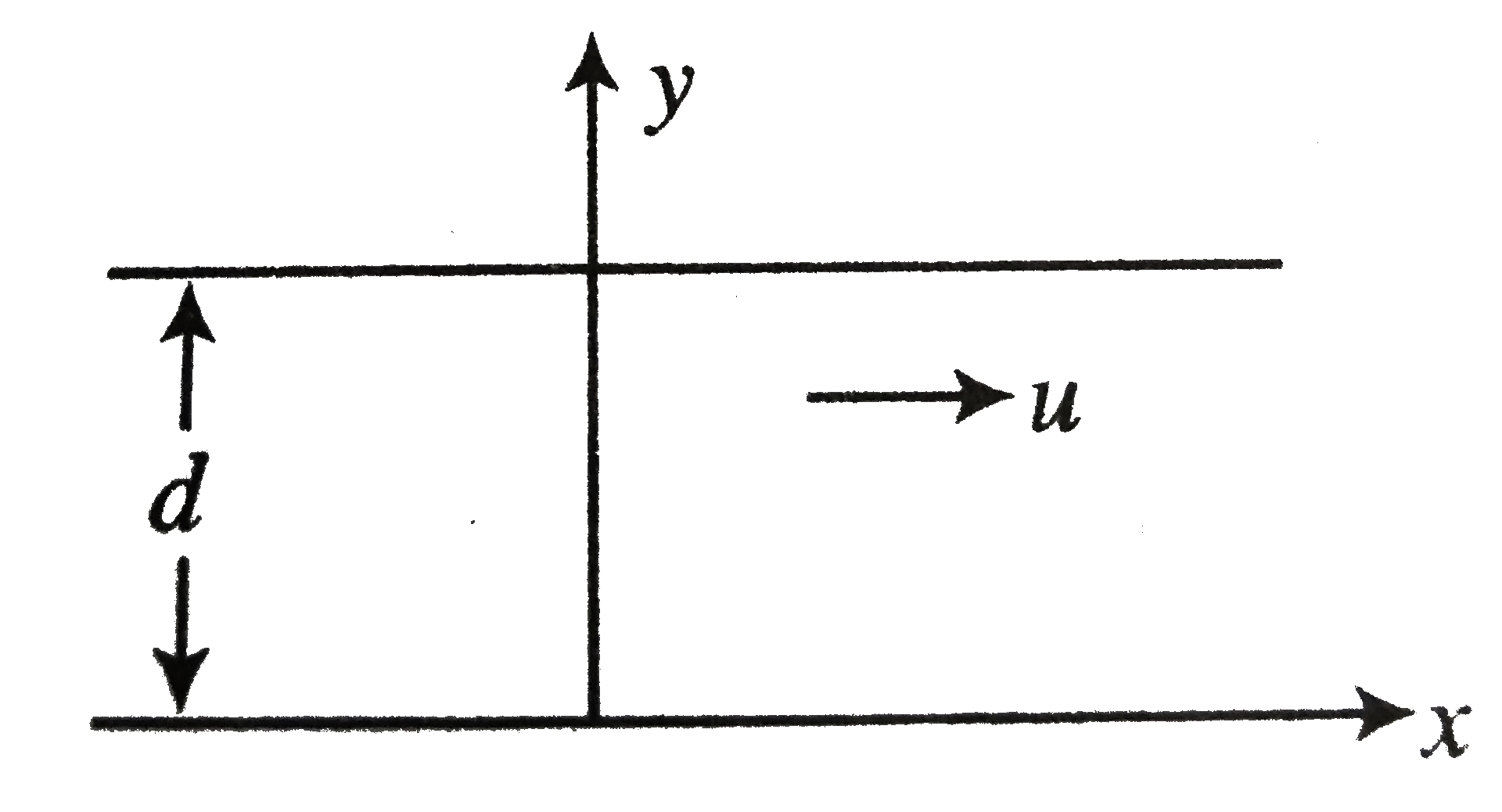
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
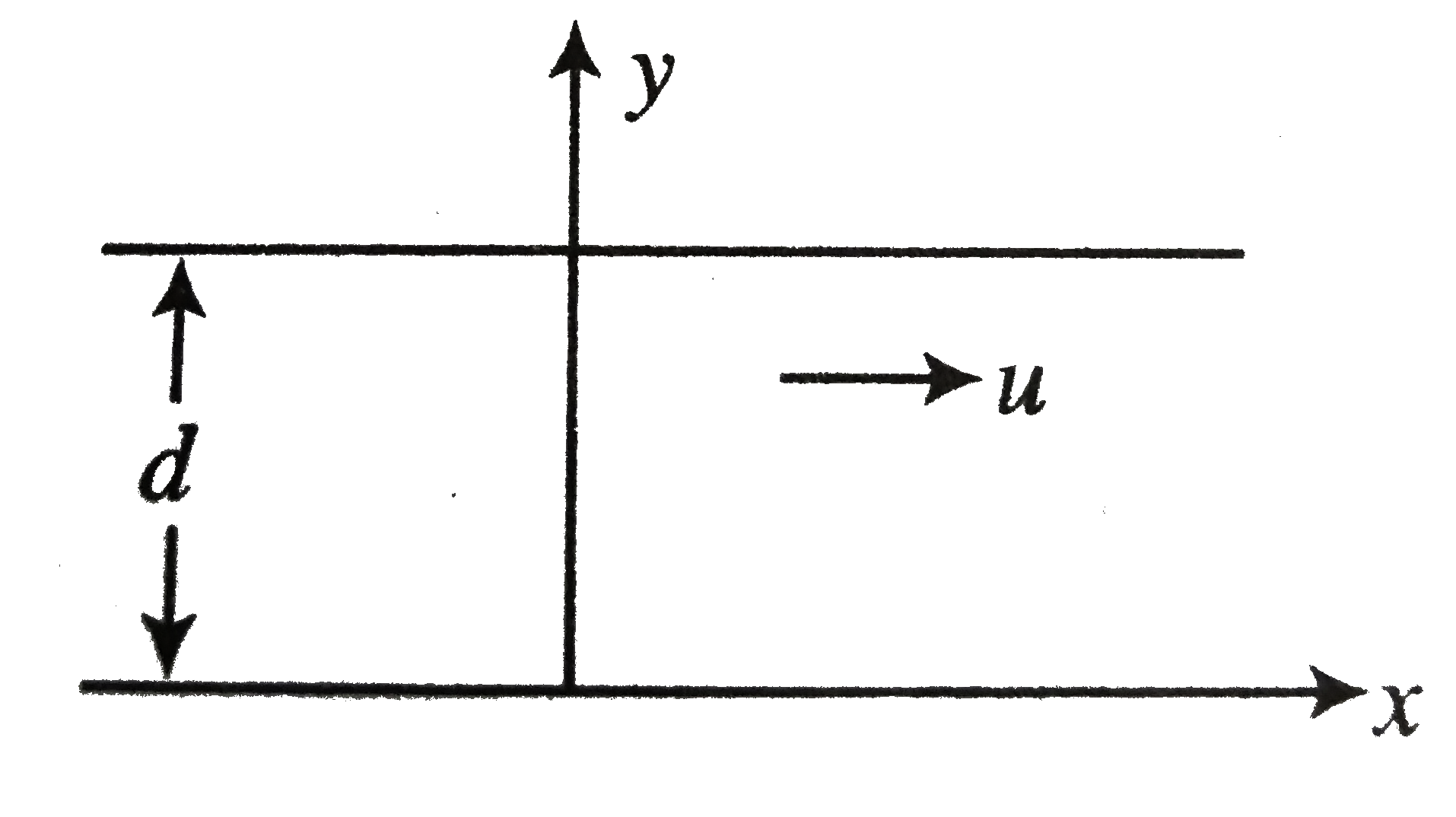
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWidth of a river is 30m, velocity is 4m/s and rowing velocity is 5m/s
(a) Make the velocity diagram for crossing the river in shortest time. Then, find this shortest time, net velocity of boatman and drigt along the river.
(b) Can the boatman reach a point just oppsite on the other shore? If yes then make the velocity diagram, the direction in which the should row his boat and the time taken to cross the river in this case.
(c) How long will it iake hom to row 10m up the stream and then back to his starting point?
View SolutionA 400m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View Solution
