A person swims at 135° to current of river, to meet target on reaching opposite point. The ratio of person's velocity to river water velocity is
√3:1
√2:1
1:√2
1:√3
The correct Answer is:B
To solve the problem of finding the ratio of the swimmer's velocity to the river's velocity when the swimmer swims at an angle of 135° to the current, we can follow these steps:
1. Understanding the Angles:
The swimmer swims at an angle of 135° with respect to the direction of the river current. This means that the swimmer's velocity vector forms a 135° angle with the river's velocity vector.
2. Components of the Swimmer's Velocity:
Let Vp be the swimmer's velocity and Vr be the river's velocity. We can break down the swimmer's velocity into its horizontal and vertical components:
- The horizontal component (against the current) is given by:
Vpx=Vpcos(135°)
- The vertical component (across the river) is given by:
Vpy=Vpsin(135°)
3. Using Trigonometric Values:
The cosine and sine of 135° can be calculated:
cos(135°)=−1√2,sin(135°)=1√2
4. Setting Up the Equation:
Since the swimmer aims to reach a point directly across the river, the horizontal component of the swimmer's velocity must equal the river's velocity:
Vr=−Vpcos(135°)
Substituting the value of cos(135°):
Vr=−Vp(−1√2)=Vp√2
5. Finding the Ratio:
To find the ratio of the swimmer's velocity to the river's velocity, we rearrange the equation:
VpVr=√2
6. Final Answer:
Thus, the ratio of the swimmer's velocity to the river's velocity is:
VpVr=√2:1
The swimmer swims at an angle of 135° with respect to the direction of the river current. This means that the swimmer's velocity vector forms a 135° angle with the river's velocity vector.
Let Vp be the swimmer's velocity and Vr be the river's velocity. We can break down the swimmer's velocity into its horizontal and vertical components:
- The horizontal component (against the current) is given by:
Vpx=Vpcos(135°)
- The vertical component (across the river) is given by:
Vpy=Vpsin(135°)
The cosine and sine of 135° can be calculated:
cos(135°)=−1√2,sin(135°)=1√2
Since the swimmer aims to reach a point directly across the river, the horizontal component of the swimmer's velocity must equal the river's velocity:
Vr=−Vpcos(135°)
Substituting the value of cos(135°):
Vr=−Vp(−1√2)=Vp√2
To find the ratio of the swimmer's velocity to the river's velocity, we rearrange the equation:
VpVr=√2
Thus, the ratio of the swimmer's velocity to the river's velocity is:
VpVr=√2:1
Similar Questions
A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
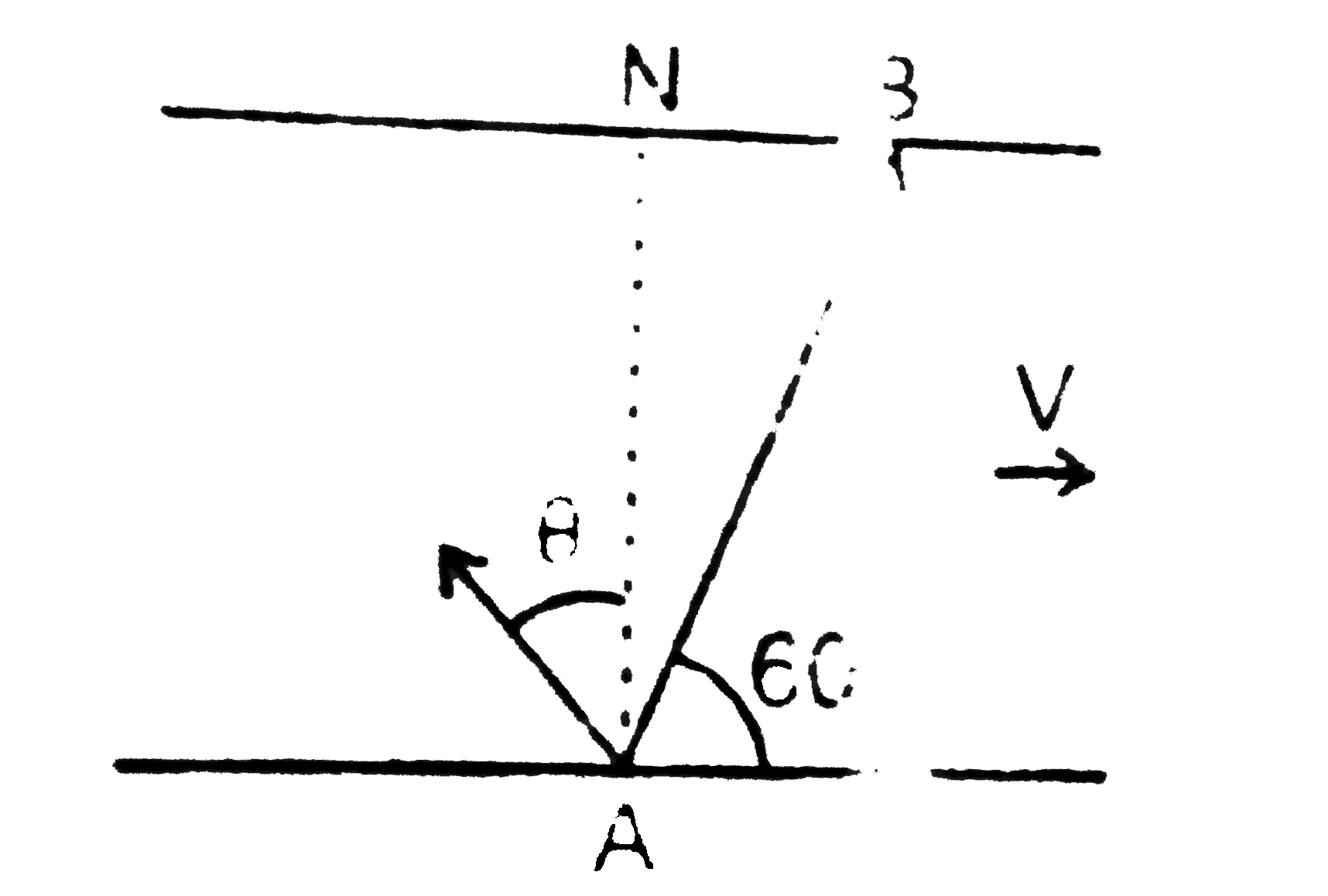
View SolutionA boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
View SolutionThe ratio of downstream drift of a person in crossing a river making same angles with downstream and upstream are respectively 2 : 1. The ratio of the speed of river u and the swimming speed of person v is:
View SolutionTwo swimmers start at the same time from point A one bank of a river to reach point B on the other bank, lying directly oppostie to point A. one of them crosses the river along the straight line AB, while the other swims at right angles to the stream and then walks the distance, which he has been carried awayby the stream to get to point B. Both swimmers reach point B at the same time. what was the velocity (assumed uniform) of his walking if velocity of both the swimmers in still water is 2.5 km h−1 and the stream velocity is 2 km h−1?

View SolutionA man can swim at 4 m/s in a still water swimming pool. He enters a 200 m wide river at one bank and swims ( w.r.t water) at an angle of 60∘ to the river flow velocity. The river flow velocity is 5 m/s . In how much -time does he cross the river ? Calculate his drift.
View SolutionA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river water is 5ms. Swimmer takes 12 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
View SolutionA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river water is 5ms. Swimmer takes 12 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
View SolutionThe width of river is 1 km. The velocity of boat is 5 km/hr. The boat covered the width of river with shortest will possible path in 15 min. Then the velocity of river stream is:
View SolutionTwo persons P and Q crosses the river starting from point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5 kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
View Solution
