The greater and least resultant of two forces are 9 N and 5 N respectively. If they are applied at 60°. The magnitude of the resultant is
100N
119N
√119 N
√67 N
The correct Answer is:D
To solve the problem, we need to find the magnitude of the resultant of two forces, F1 and F2, given that the greatest resultant is 9 N, the least resultant is 5 N, and the angle between the forces is 60°.
1. Define the Forces:
Let F1 be the greater force and F2 be the lesser force. According to the problem, we have:
F1+F2=9N(1)
F1−F2=5N(2)
2. Solve the Equations:
To find F1 and F2, we can add equations (1) and (2):
(F1+F2)+(F1−F2)=9+5
This simplifies to:
2F1=14⟹F1=7N
Now, substitute F1 back into equation (1) to find F2:
7+F2=9⟹F2=2N
3. Calculate the Resultant at 60°:
Now that we have F1=7N and F2=2N, we can calculate the resultant R when the angle θ=60°:
R=√F21+F22+2F1F2cos(60°)
Substitute the values:
R=√72+22+2⋅7⋅2⋅12
Simplifying further:
R=√49+4+14
R=√67
4. Final Result:
Therefore, the magnitude of the resultant is:
R=√67N
Let F1 be the greater force and F2 be the lesser force. According to the problem, we have:
F1+F2=9N(1)
F1−F2=5N(2)
To find F1 and F2, we can add equations (1) and (2):
(F1+F2)+(F1−F2)=9+5
This simplifies to:
2F1=14⟹F1=7N
7+F2=9⟹F2=2N
Now that we have F1=7N and F2=2N, we can calculate the resultant R when the angle θ=60°:
R=√F21+F22+2F1F2cos(60°)
Substitute the values:
R=√72+22+2⋅7⋅2⋅12
Simplifying further:
R=√49+4+14
R=√67
Therefore, the magnitude of the resultant is:
R=√67N
Similar Questions
The greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60°. The magnitude of the resultant is
View SolutionThe maximum and minimum magnitudes of the resultant of two forces are 5 N and 5N respectively. Find the magnitude of resultant force when act orthogonally to each other.
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
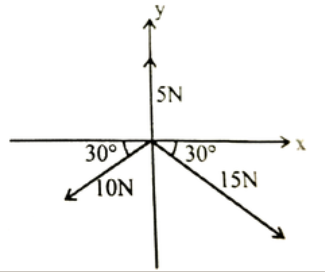
Find the magnitude of the resultant of shown forces :-
View SolutionThe greatest and least resultant of two forces acting at a point is 29 kgwt and 5 kgwt respectively . If each force is increased by 3 kgwt , find the resultant of the two new forces when acting at right angles to each other ?
View SolutionThe magnitudes of mutually perpendicular forces a,b and c are 2,10 and 11 respectively. Then the magnitude of its resultant is
View SolutionThe greatest & the least magnitude of the resultant of two forces of constant magnitudes are P & Q respectively. If the forces act at an angle 2α, then prove that the magnitude of their resultant is given by √P2cos2α+Q2sin2α.
View SolutionTwo equal forces of magnitude 'p' each are angled first at 60° later at 120°. The ratio of magnitude of their resultants is
View SolutionThe maximum and minimum magnitudes of the resultant of two vectors are 23 units and 7 units respectively. If these two vectors are acting at right angles to each other, the magnitude of their resultant will be
View SolutionThe maximum and minimum magnitudes of the resultant of two vectors are 23 units and 7 units respectively. If these two vectors are acting at right angles to each other, the magnitude of their resultant will be
View Solution
