Two equal forces of magnitude 'p' each are angled first at 60° later at 120°. The ratio of magnitude of their resultants is
1:√3
√3:1
1:1
1:2
The correct Answer is:B
To solve the problem of finding the ratio of the magnitudes of the resultant forces when two equal forces of magnitude 'p' are angled first at 60° and later at 120°, we can follow these steps:
Step 1: Calculate the Resultant for 60°
1. Identify the forces and the angle: Let the two forces be F1=p and F2=p with an angle θ1=60° between them.
2. Use the formula for the resultant: The magnitude of the resultant R1 of two forces can be calculated using the formula:
R1=√F21+F22+2F1F2cos(θ1)
3. Substitute the values:
R1=√p2+p2+2⋅p⋅p⋅cos(60°)
Since cos(60°)=12:
R1=√p2+p2+2⋅p2⋅12=√2p2+p2=√3p2=√3p
Step 2: Calculate the Resultant for 120°
1. Identify the angle: Now, let’s consider the same forces with an angle θ2=120°.
2. Use the formula for the resultant: The magnitude of the resultant R2 is given by:
R2=√F21+F22+2F1F2cos(θ2)
3. Substitute the values:
R2=√p2+p2+2⋅p⋅p⋅cos(120°)
Since cos(120°)=−12:
R2=√p2+p2+2⋅p2⋅(−12)=√2p2−p2=√p2=p
Step 3: Find the Ratio of the Resultants
1. Calculate the ratio:
Ratio=R1R2=√3pp=√3
2. Express the ratio:
R1:R2=√3:1
Final Answer
The ratio of the magnitudes of their resultants is √3:1.
---
1. Identify the forces and the angle: Let the two forces be F1=p and F2=p with an angle θ1=60° between them.
2. Use the formula for the resultant: The magnitude of the resultant R1 of two forces can be calculated using the formula:
R1=√F21+F22+2F1F2cos(θ1)
3. Substitute the values:
R1=√p2+p2+2⋅p⋅p⋅cos(60°)
Since cos(60°)=12:
R1=√p2+p2+2⋅p2⋅12=√2p2+p2=√3p2=√3p
1. Identify the angle: Now, let’s consider the same forces with an angle θ2=120°.
2. Use the formula for the resultant: The magnitude of the resultant R2 is given by:
R2=√F21+F22+2F1F2cos(θ2)
3. Substitute the values:
R2=√p2+p2+2⋅p⋅p⋅cos(120°)
Since cos(120°)=−12:
R2=√p2+p2+2⋅p2⋅(−12)=√2p2−p2=√p2=p
1. Calculate the ratio:
Ratio=R1R2=√3pp=√3
2. Express the ratio:
R1:R2=√3:1
The ratio of the magnitudes of their resultants is √3:1.
Similar Questions
Two forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionTwo equal forces (P each) act at a point inclined to each other at an angle of 120∘. The magnitude of their resultant is
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
When two vectors of magnitudes P and Q are inclined at an angle θ, the magnitudes of their resultant is 2P. When the inclination is changed to 180∘−θ, the magnitudes of the resultant is halved. Find the ratio of P and Q.
View SolutionTwo forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
View SolutionTwo vectors having equal magnitude of 5 units, have an angle of 60∘ between them. Find the magnitude of their resultant vector and its angle from one of the vectors.

View SolutionFind the magnitude of the resultant of shown forces :-
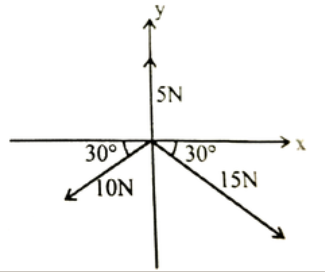
View SolutionThe resultant of two vectors , having equal magnitudes E make an angle of 120∘ with each other . What is the magnitude and direction of the resultant ?
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
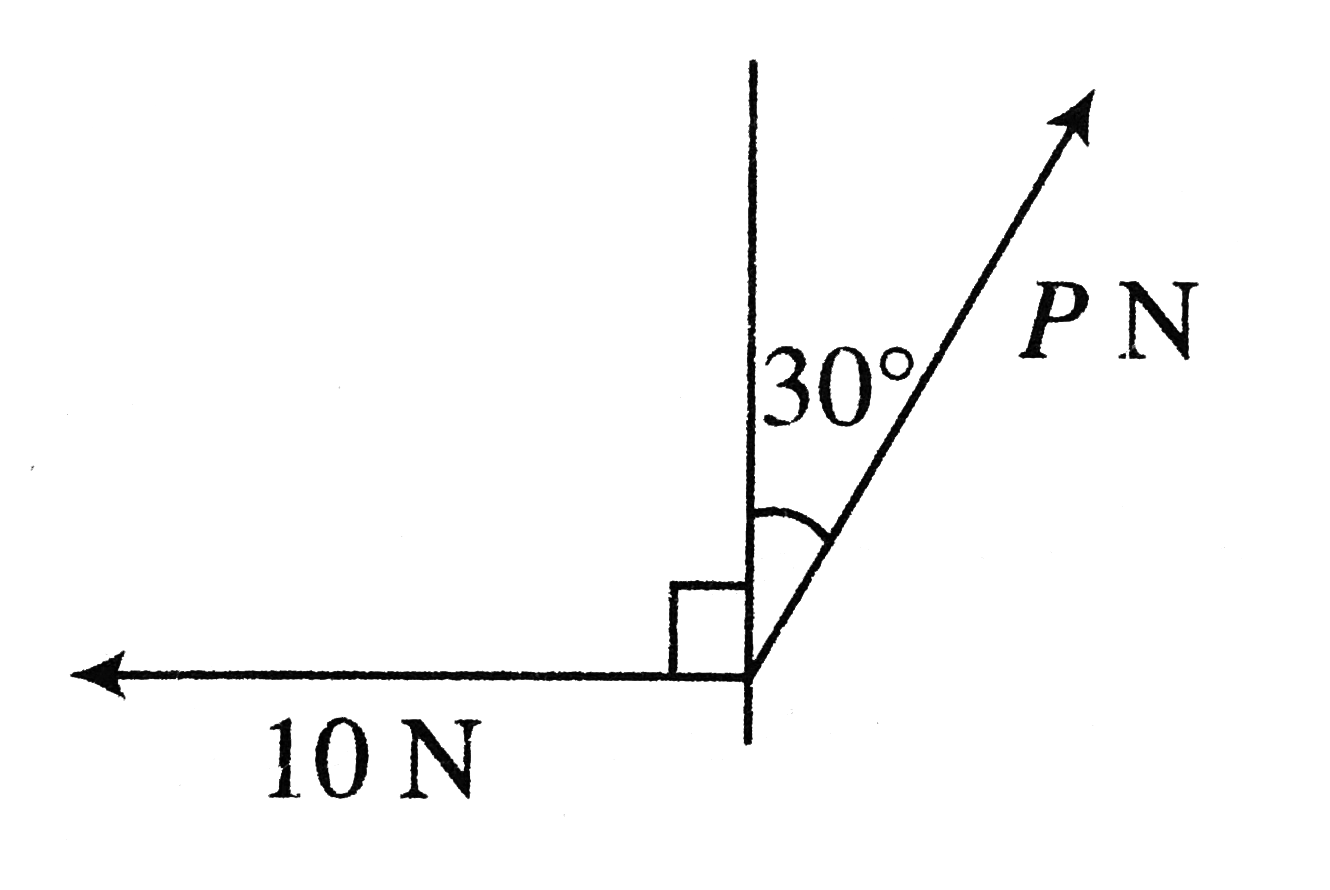
View SolutionThe greater and least resultant of two forces are 9 N and 5 N respectively. If they are applied at 60°. The magnitude of the resultant is
View Solution
