When a thin transparent plate of Refractive Index 1.5 is introduced in one of the interfearing becomes, 20 fringes shift. If it is replaced by another thin plate of half the thickness and of R.I 1.7 the number of fringes that undergo displacement is
23
14
28
7
The correct Answer is:B
To solve the problem step-by-step, we will use the formula for the number of fringes shifted in an interference pattern when a thin transparent plate is introduced.
Step 1: Understand the formula for fringe shift
The number of fringes shifted (n) when a thin transparent plate of thickness t and refractive index μ is introduced is given by:
n=(μ−1)⋅tλ
where λ is the wavelength of the light used.
Step 2: Calculate the number of fringes shifted for the first plate
For the first plate:
- Refractive index μ1=1.5
- Let the thickness of the plate be t.
- The number of fringes shifted is given as n1=20.
Using the formula:
n1=(1.5−1)⋅tλ=0.5⋅tλ
We can express this as:
20=0.5⋅tλ(1)
Step 3: Set up the equation for the second plate
For the second plate:
- Refractive index μ2=1.7
- The thickness of the second plate is half of the first, so t2=t2.
Using the same formula for the second plate:
n2=(1.7−1)⋅t2λ=(0.7)⋅t2λ
This simplifies to:
n2=0.7⋅t2λ(2)
Step 4: Relate the two equations
From equation (1), we have:
tλ=40(from rearranging 20 = 0.5 * t / λ)
Now substituting this into equation (2):
n2=0.7⋅(40λ)2λ
The λ cancels out:
n2=0.7⋅402=282=14
Conclusion
The number of fringes that undergo displacement when the second plate is introduced is approximately 14.
The number of fringes shifted (n) when a thin transparent plate of thickness t and refractive index μ is introduced is given by:
n=(μ−1)⋅tλ
where λ is the wavelength of the light used.
For the first plate:
- Refractive index μ1=1.5
- Let the thickness of the plate be t.
- The number of fringes shifted is given as n1=20.
n1=(1.5−1)⋅tλ=0.5⋅tλ
We can express this as:
20=0.5⋅tλ(1)
For the second plate:
- Refractive index μ2=1.7
- The thickness of the second plate is half of the first, so t2=t2.
n2=(1.7−1)⋅t2λ=(0.7)⋅t2λ
This simplifies to:
n2=0.7⋅t2λ(2)
From equation (1), we have:
tλ=40(from rearranging 20 = 0.5 * t / λ)
n2=0.7⋅(40λ)2λ
The λ cancels out:
n2=0.7⋅402=282=14
The number of fringes that undergo displacement when the second plate is introduced is approximately 14.
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) (straight objective Type Questions)
31 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions
4 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
In a Young.s double slit experiment, the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
View SolutionIn YDSE, the sources is red ligth of wavelength 7×10−7m. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by 10−3 m to the position previously occupied by the 5th bright fringe.
What is the thickness of the plate?
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View SolutionIn YDSE, the sources is red ligth of wavelength 7×10−7m. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by 10−3 m to the position previously occupied by the 5th bright fringe.
If the source is now changed to green light of wavelength 10−7m, the central fringe shifts to a position initially occupied by the sixth bright fringe due to red ligth. What will be refractive index of glass plate for the second ligth for changed source of ligth?
View SolutionWhen a mica plate of thickness 0.1mm is introduced in one of the interfering beams, the central fringe is displaced by a distance equal to 10 fringes. If the wavelength of the light is 6000A0, the refractive index of the mica is
View SolutionInterference fringes are produced by a double slit arrangement
and a piece of plane parallel glass of refractive index 1.5 is interposed in one of
the interfering beam. If the fringes are displaced through 30 fringe widths for
light of wavelength 6×10−5cm, find the thickness of the plate.
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionTo make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement.
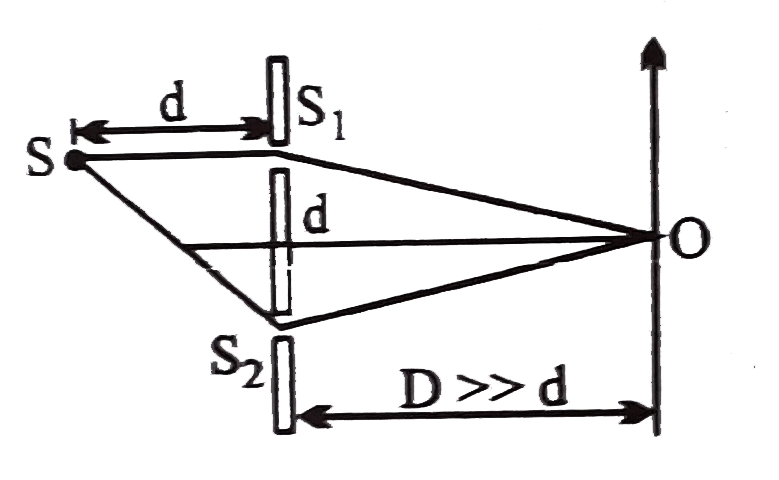
View SolutionIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
View SolutionInterference pattern with Young's double slits 1.5mm apart are formed on a screen at a distance 1.5m from the plane of slits. In the path of the beam of one of the slits, a transparent film of 10 micron thickness and of refractive index 1.6 is interposed while in the path of the beam from the older slit a transparent film of 15 micron thickness and of refractive index 1.2 is interposed. Find the displacement of the fringe patten.
View Solution
