Two transparent slabs having equal thickness 0.45 mm and refractive indices 1.40 and 1.42 are pasted on the two slits of a double slit apparatus. The separation of slits equals 1mm. Wavelength of light used equals 600 nm. The screen is placed at a distance 1m from the plane of the slits. The central maxima from the centre of the screen is [in mm]
The correct Answer is:9
To solve the problem step by step, we will analyze the given information and apply the principles of wave optics.
Given Data:
- Thickness of each slab, t=0.45mm=0.45×10−3m
- Refractive indices: n1=1.40, n2=1.42
- Separation of slits, d=1mm=1×10−3m
- Wavelength of light, λ=600nm=600×10−9m
- Distance from slits to screen, L=1m
Step 1: Calculate the Optical Path Length Difference
The optical path length for a medium is given by:
Optical Path Length=n⋅t
For the first slab (with n1=1.40):
OPL1=n1⋅t=1.40⋅0.45×10−3m=0.000630m
For the second slab (with n2=1.42):
OPL2=n2⋅t=1.42⋅0.45×10−3m=0.000639m
Step 2: Calculate the Path Difference
The path difference (Δx) due to the slabs is:
Δx=OPL2−OPL1=0.000639m−0.000630m=0.000009m=9μm
Step 3: Relate Path Difference to Position on the Screen
The path difference can also be expressed in terms of the position y on the screen:
Δx=d⋅yL
Setting the two expressions for path difference equal gives:
d⋅yL=9×10−6m
Step 4: Solve for y
Substituting the known values:
1×10−3⋅y1=9×10−6
y=9×10−61×10−3=0.009m=9mm
Conclusion
The position of the central maxima from the center of the screen is:
9mm
- Thickness of each slab, t=0.45mm=0.45×10−3m
- Refractive indices: n1=1.40, n2=1.42
- Separation of slits, d=1mm=1×10−3m
- Wavelength of light, λ=600nm=600×10−9m
- Distance from slits to screen, L=1m
The optical path length for a medium is given by:
Optical Path Length=n⋅t
For the first slab (with n1=1.40):
OPL1=n1⋅t=1.40⋅0.45×10−3m=0.000630m
For the second slab (with n2=1.42):
OPL2=n2⋅t=1.42⋅0.45×10−3m=0.000639m
The path difference (Δx) due to the slabs is:
Δx=OPL2−OPL1=0.000639m−0.000630m=0.000009m=9μm
The path difference can also be expressed in terms of the position y on the screen:
Δx=d⋅yL
Setting the two expressions for path difference equal gives:
d⋅yL=9×10−6m
Substituting the known values:
1×10−3⋅y1=9×10−6
y=9×10−61×10−3=0.009m=9mm
The position of the central maxima from the center of the screen is:
9mm
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise (Practice Sheet (Advanced))
6 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions
16 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Matrix Matching Type Questions
1 Video
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Two slits are separated by a distance of 0.5mm and illuminated with light of λ=6000Å. If the screen is placed 2.5m from the slits. The distance of the third bright image from the centre will be
View SolutionTwo transparent slabs having equal thickness but different refractive indices μ1andμ2, are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits ?
View SolutionIn a Young's double slit experiment the separation between the slits is 0.10 mm, the wavelength of light used is 600 nm and the interference pattern is observed on a screen 1.0 m away. Find the separation between the successive bright fringes.
View SolutionIn a YDSE, distance between the slits and the screen is 1m, separation between the slits is 1mm and the wavelength of the light used is 5000nm. The distance of 100th maxima from the central maxima is:
View SolutionIn the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
View SolutionIn the youngs double slit experiment ,the slit sepration is 1mm ,the distance between source and screen is 1m ,wavelength of light used is 6500 angstrom.Find the distance between fifth maxima and third minima in (mm)?
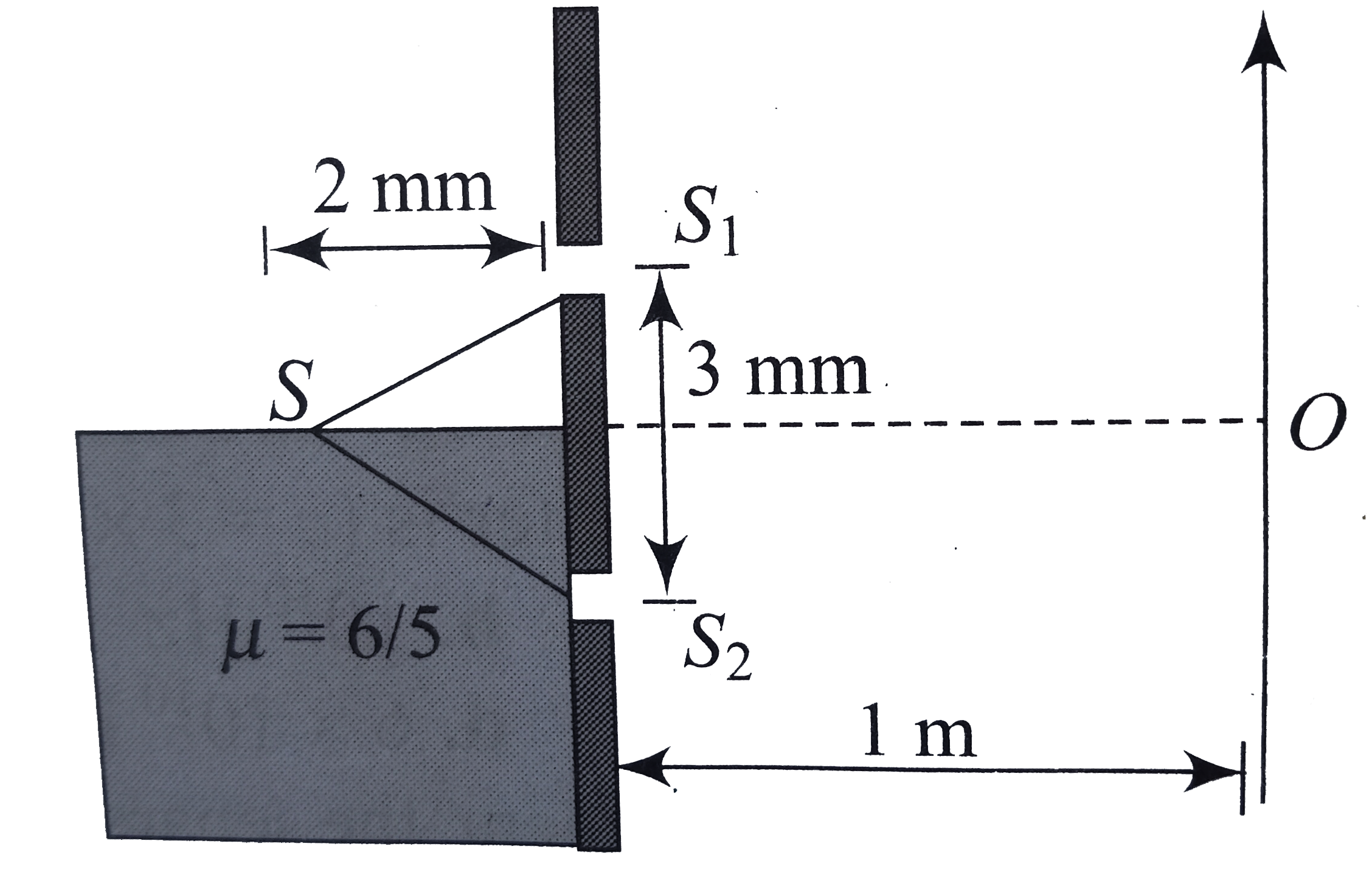
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View SolutionIn YDSE a=2mm, D = 2m, λ=500 nm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn YDSE, the two slits are separated by 0.1mm and they are 0.5m from the screen. The wavelenght of light used is 5000A0. Find the distance between 7th maxima 11th minima on the screen.
View Solution
