When a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
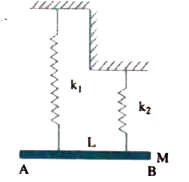
As it given that the mass M stretches the original spring by a distance x,
we have kx=Mg (or) k=Mgx......... (1)
The new force constants of the two springs can be given by using equations
k1=kegll1andk2=keqll2as,k1=3kandk2=3k2
Let we take the stretch in the two springs be x1andx2 we have for the equilibrium of the rod
k1x1+k2x2=Mg (or) 2kx1+3k2x2=Mg
From equation (1) , we have x1+x22=x3......... (2)
As the rod is horizontal and in static equilibrium , we have net torque acting on the rod about any point on it must be zero. Thus we have torquie on it above end A are
k2x2L=Mg(L)2
(or) x2=Mg2k2=Mg3k=x3
Using this value of x2 in equation (2) ,
we have x1=x6
This can also be directly obtained by using torque zero about point B on the rod as
k1x1L=Mg(L)2
(or) x1=Mg2k1=Mg6k=x6
Similar Questions
A spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View SolutionTime period of a block with a spring is T0. Now ,the spring is cut in two parts in the ratio 2:3. Now find the time period of same block with the smaller part of the spring.
View SolutionA mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
View SolutionA mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
View SolutionIf a spring of stiffness 'k' is cut into two parts 'A' and 'B' of length lA:lB=2:3, then the stiffness of spring 'A' is given by
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
 View Solution
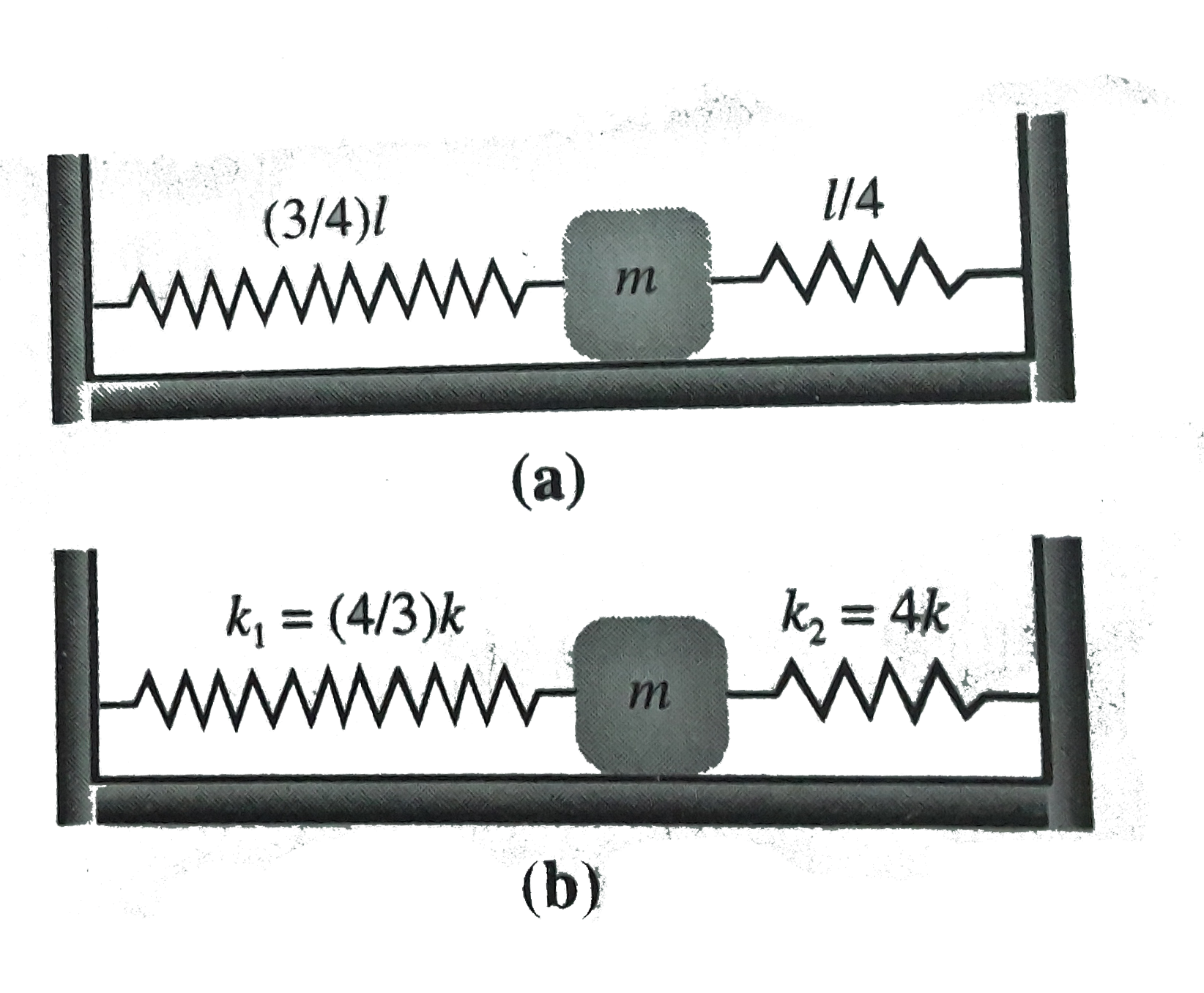
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
 View Solution
View SolutionThe time period of a spring mass system of spring constant k and mass m is T. Now, the spring is cut into two equal parts and connected in parallel. If the same mass is attached to new arrangement, then new time period is
View Solution

