Check the correctness of the formula S=ut+13at2 where S is the distance , u is velocity , a is acceleration and t is time.
Dimensionally LHS= [L]
RHS =[LT−1][T]+[LT−2][T]2
[L]+[L]=[L]
Since, the dimension of each term on both sides are same, the given equation is dimensionally correct.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -1 A
187 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE- 1 B
28 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
7 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
Chek the correctness of the relation, Snth=u+a2(2n−1), where u is initial velocity, a is acceleratin and Snth is the distance travelled by the body in nth second.
View SolutionCheck the correctness of following equation by the method of dimensions :
S=ut+12at2 .
where S is the distance covered bu a body in time t, having initial velocity u and acceleration a.
View SolutionCheck the correctness of the equations (i) s=ut+12at2 (ii) v2=u2+2as using dimensions.
View SolutionA particle starts rotating from rest according to the formula θ=(t2/64)−(t/8) where θ is the angle in radian and t in s . Find the angular velocity and angular acceleration at the end of 4 s .
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View Solution(a) Write a equation of motion in different states and derive the relation :
s=u+12a(2t−1)
Where, s is the distance covered in tth second, u is initial velocity and a is uniform acceleration.
View SolutionThe distance travelled by a particle in nth second is Sn=u+a2(2n−1) where u is the velocity and a is the acceleration. The equation is
View SolutionFigure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
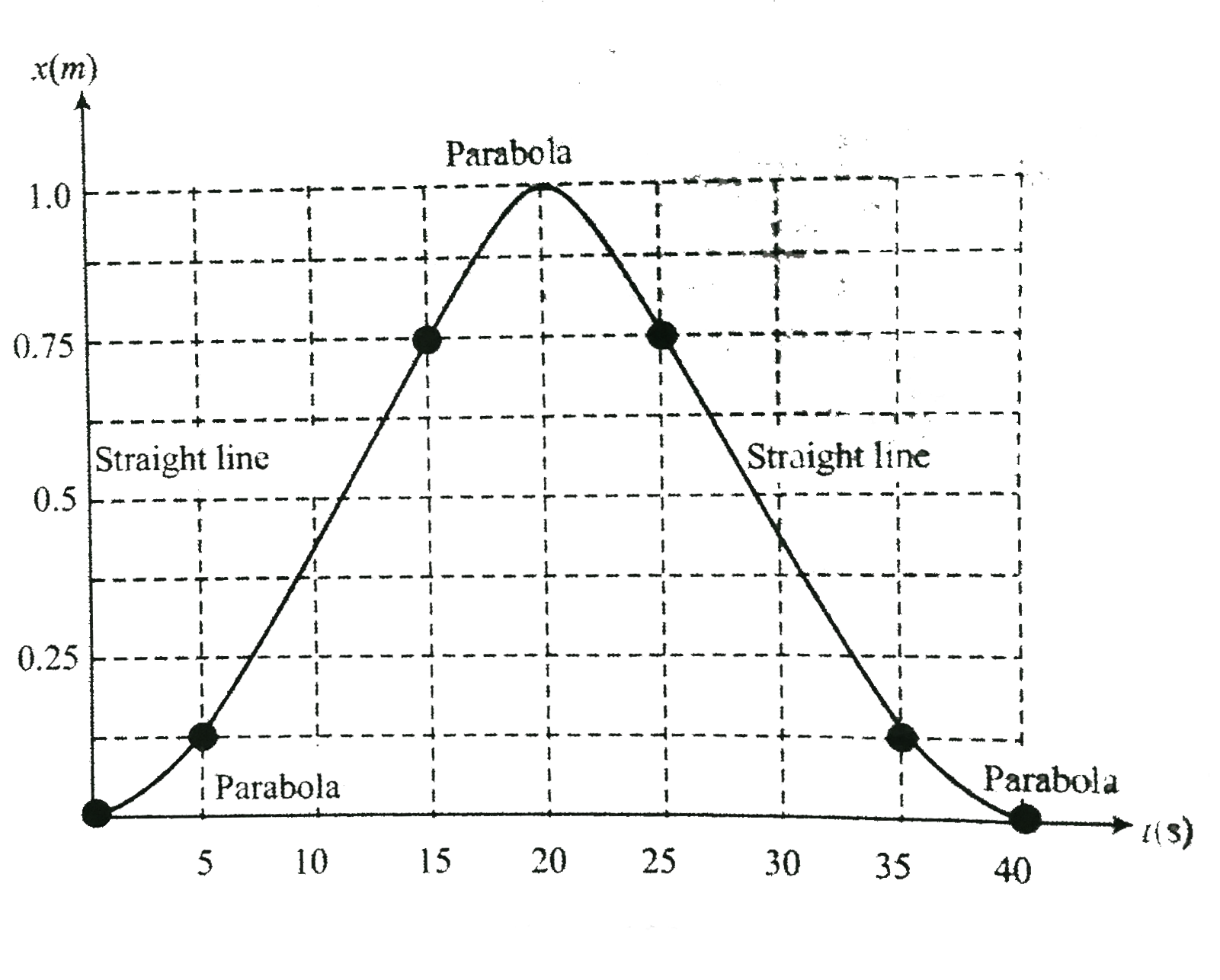 .
.
View SolutionA car is running on a straight road . The distance travelled and time taken are connected by the formula =t2−2t where t is measured in hours and s in km. When the odometer reading is 15, what is the speedometer reading ? [ Odometer measures s and the speedmeter measures velocity]
View Solution
