Read the each statement below carefully and state, with reasons, if it is true or false:
a) The net acceleration of a particle in circular motimn is always along the radius of the circle towards the center.
b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
A only true
B only true
Both A & B are true
Both A & B are false
The correct Answer is:B
Step by step video & image solution for Read the each statement below carefully and state, with reasons, if it is true or false: a) The net acceleration of a particle in circular motimn is always along the radius of the circle towards the center. b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point. c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A ( Vector & scalar)
2 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Resolution, motion in plane and motion of boat
4 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Relative velocity)
18 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Read each statement below carefully and state, with reasons, if it is true or false :
(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the center.
(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
View SolutionThe acceleration vector of a particle in uniform circular motion averaged over the cycle is a null vector. This statement is
View Solution
Knowledge Check
A particle revolves round a circular path with uniform speed. The acceleration of the particle is
Aalong the circumference of the circle.Balong the tangentCalong the radiusDzero
Read each statement below carefully and state with reason and examples, if it is true or false. A scalar quantity is one that
View SolutionRead each statement below carefully and state with reasons, with it is true or false :
(a) The magnitude of vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e) three vectors not lying in a plane can never add up to give a null vector.
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
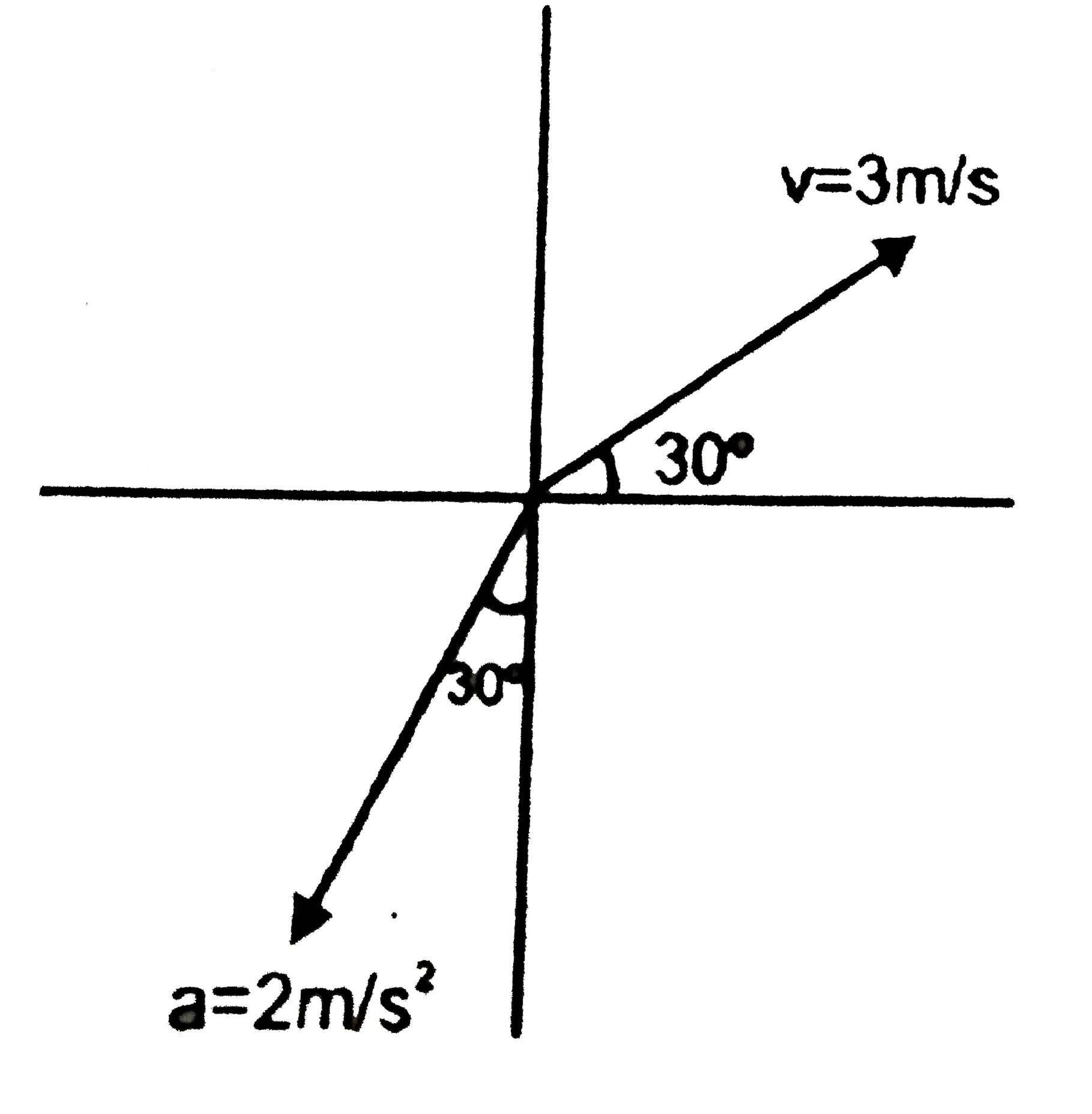
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
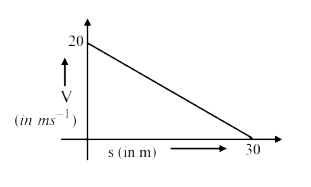
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View Solution
