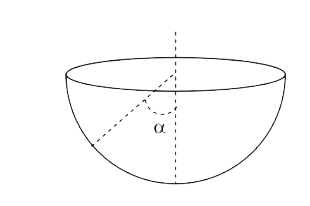
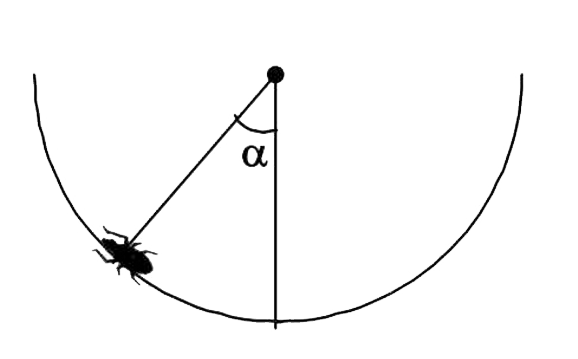
An insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
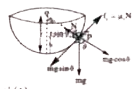
N=mgcosθ………(1)
μN=mgsinθ……..(2)
From (1) and (2), we get:
cotθ=1/μ=3⇒θ=cot−1(3)
Similar Questions
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 View Solution
View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 View Solution
View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 View Solution
View SolutionAn insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
 View Solution
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
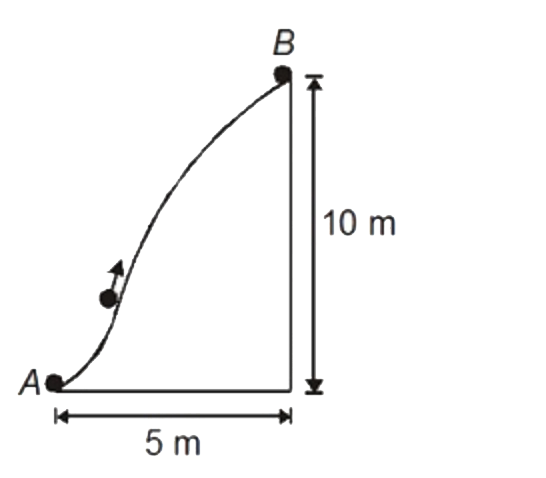
View SolutionA particle is pulled along a curved surface very slowly. The coefficient of kinetic friction between the particle and surface is 0.4 . The heat generated during the pulling of the particle from the lowest point A to the topmost point B equals (The mass of the particle is 5 g )
 View Solution
View SolutionIf the coefficient of friction between M and the inclined surfaces is μ=1/√3 find the minimum mass m of the rod so that the of mass M=10kg remain stationary on the inclined plane
 View Solution
View SolutionA block of mass 50 kg can slide on a rough horizontal surface. The coefficient of friction between the block and the surface is 0.6. The least force of pull acting at an
angle of 30∘ to the upwawrd drawn ve3rtical which causes the block to just slide isView Solution

