The area under force time curve gives
work
power
displacement
impluse
The correct Answer is:D
To solve the question, "The area under the force-time curve gives," we need to analyze the relationship between force, time, and impulse. Here’s a step-by-step solution:
Step 1: Understand the Force-Time Graph
- In a force-time graph, the y-axis represents force (F), and the x-axis represents time (t). The area under the curve in this graph is what we need to determine.
Hint: Remember that the area under a graph often represents a physical quantity related to the variables plotted.
Step 2: Identify the Area Under the Curve
- The area under the force-time curve can be calculated by multiplying the force by the time interval over which that force acts. If we denote the force as F and the time interval as Δt, then the area can be expressed as:
Area=F×Δt
Hint: Think about what multiplying force by time might represent in physical terms.
Step 3: Relate Area to Impulse
- In physics, impulse (J) is defined as the change in momentum of an object when a force is applied over a period of time. Mathematically, impulse is given by the formula:
J=F×Δt
- Thus, the area under the force-time curve is equal to the impulse applied to an object.
Hint: Recall the definition of impulse and how it relates to force and time.
Step 4: Conclusion
- Therefore, the area under the force-time curve gives the impulse. This means that the correct answer to the question is:
The area under the force-time curve gives impulse.
Hint: Look for the option that mentions impulse as it directly corresponds to the area under the force-time graph.
Final Answer
The area under the force-time curve gives impulse.
- In a force-time graph, the y-axis represents force (F), and the x-axis represents time (t). The area under the curve in this graph is what we need to determine.
- The area under the force-time curve can be calculated by multiplying the force by the time interval over which that force acts. If we denote the force as F and the time interval as Δt, then the area can be expressed as:
Area=F×Δt
- In physics, impulse (J) is defined as the change in momentum of an object when a force is applied over a period of time. Mathematically, impulse is given by the formula:
J=F×Δt
- Thus, the area under the force-time curve is equal to the impulse applied to an object.
- Therefore, the area under the force-time curve gives the impulse. This means that the correct answer to the question is:
The area under the force-time curve gives impulse.
The area under the force-time curve gives impulse.
Similar Questions
Knowledge Check
The area under force-displacement curve represents
AvelocityBaccelerationCimpulseDwork doneThe area under velocity-time graph for a particle in a given interval of time represnets
AvelocityBaccelerationCwork doneDDisplacement does not tell the nature of the actual motion of a particle between the points.
Find the area under the given curves and given lines:(i) y=x2,x=1,x=2and x-axis(ii) y=x4, x=1,x=5and x-axis
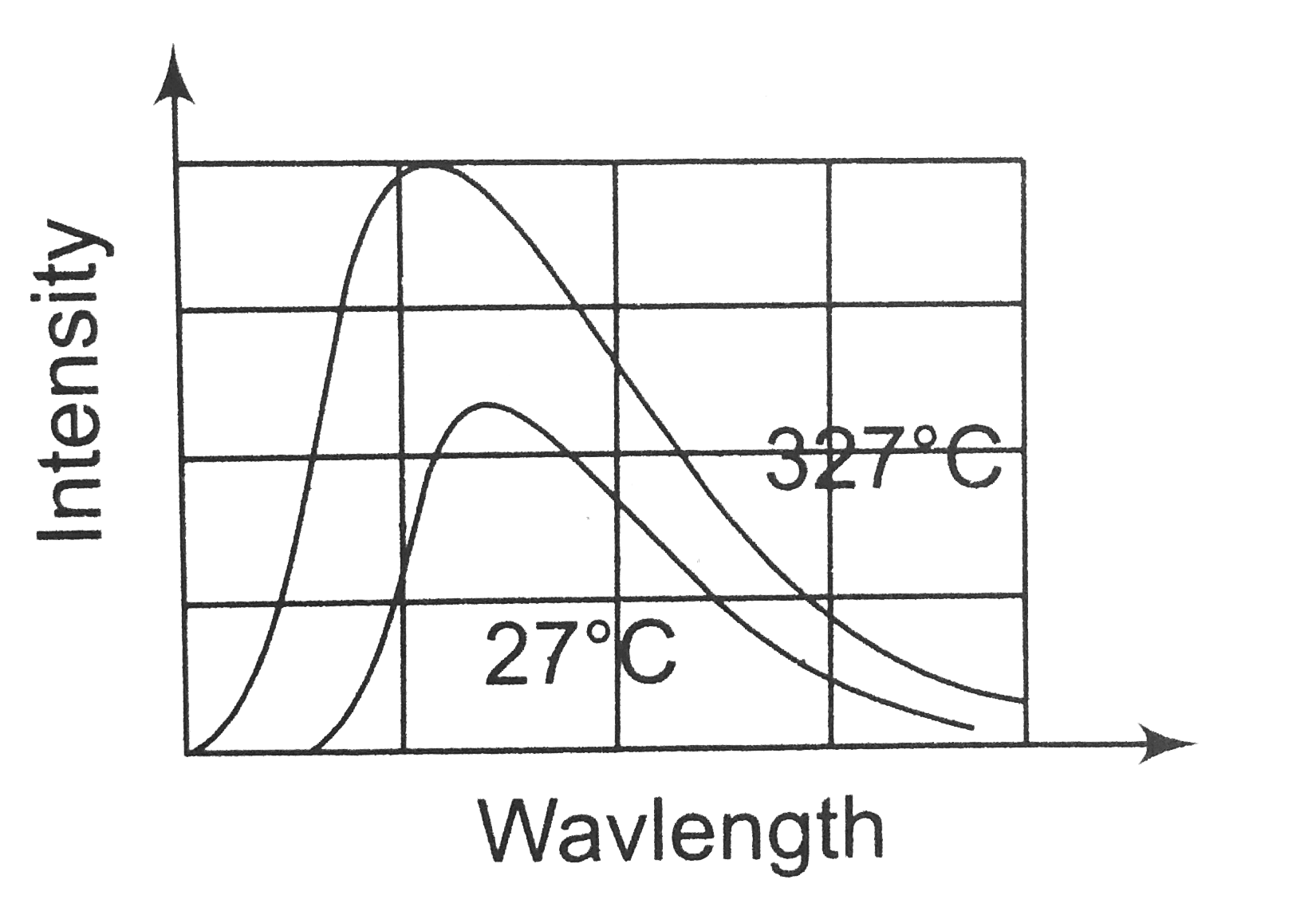
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View Solution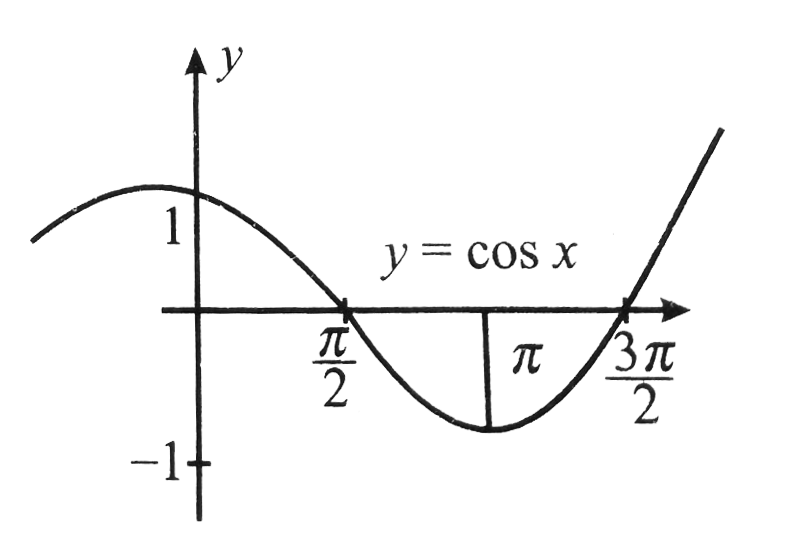
Find the area under the curve y=cosx over the interval
(a) [0,π2]
(b) [0,π]
View SolutionDraw a rough sketch of the curve y=√x−1 in the interval [1, 5] and find the area under the given curve and between the lines x = 1 and x = 5.
View SolutionFind the area under the curve y=sin2x+cos2x between the ordinates x = 0, x=π4
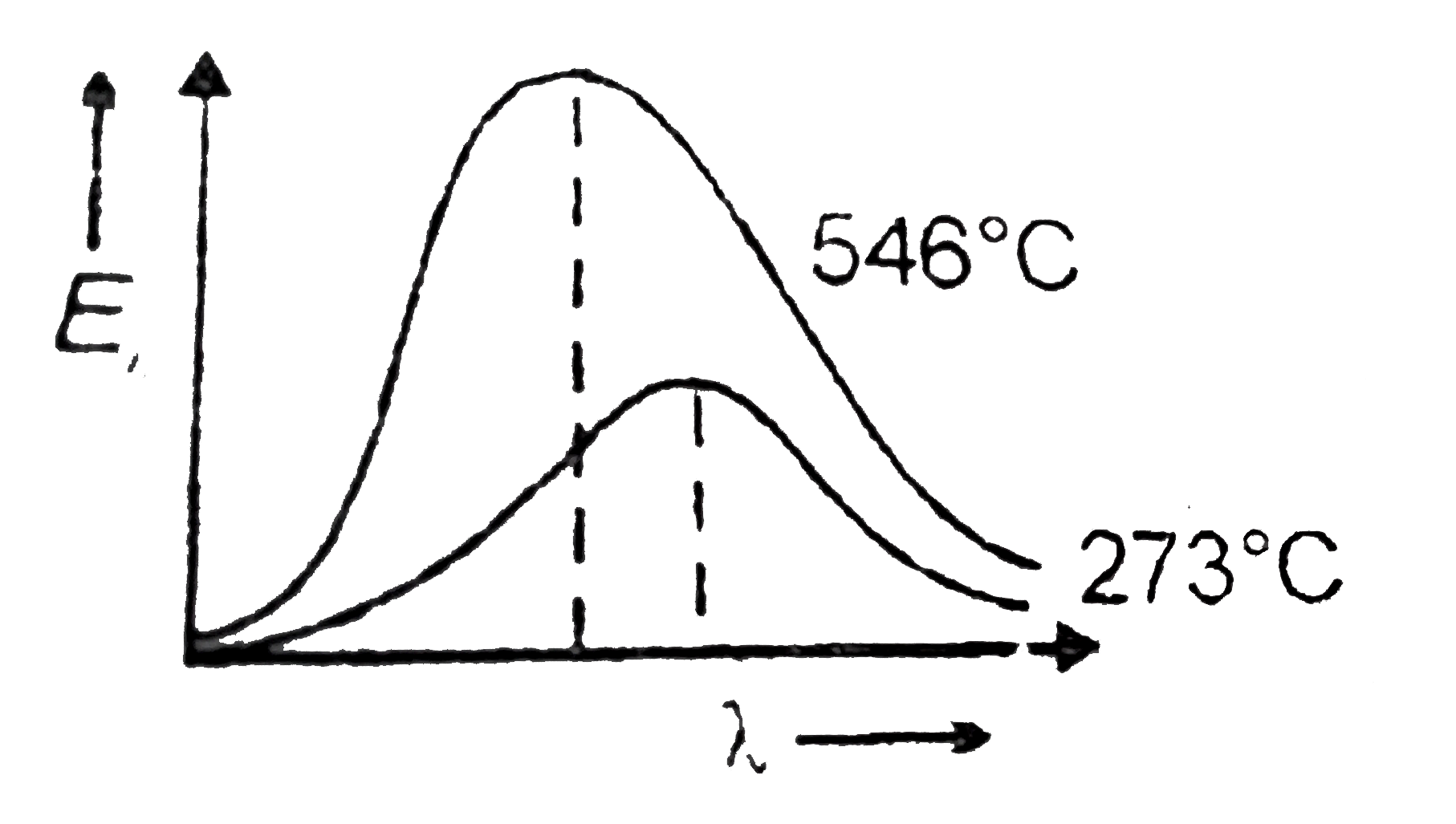
View SolutionThe spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
View Solution