Area under this given curve gives
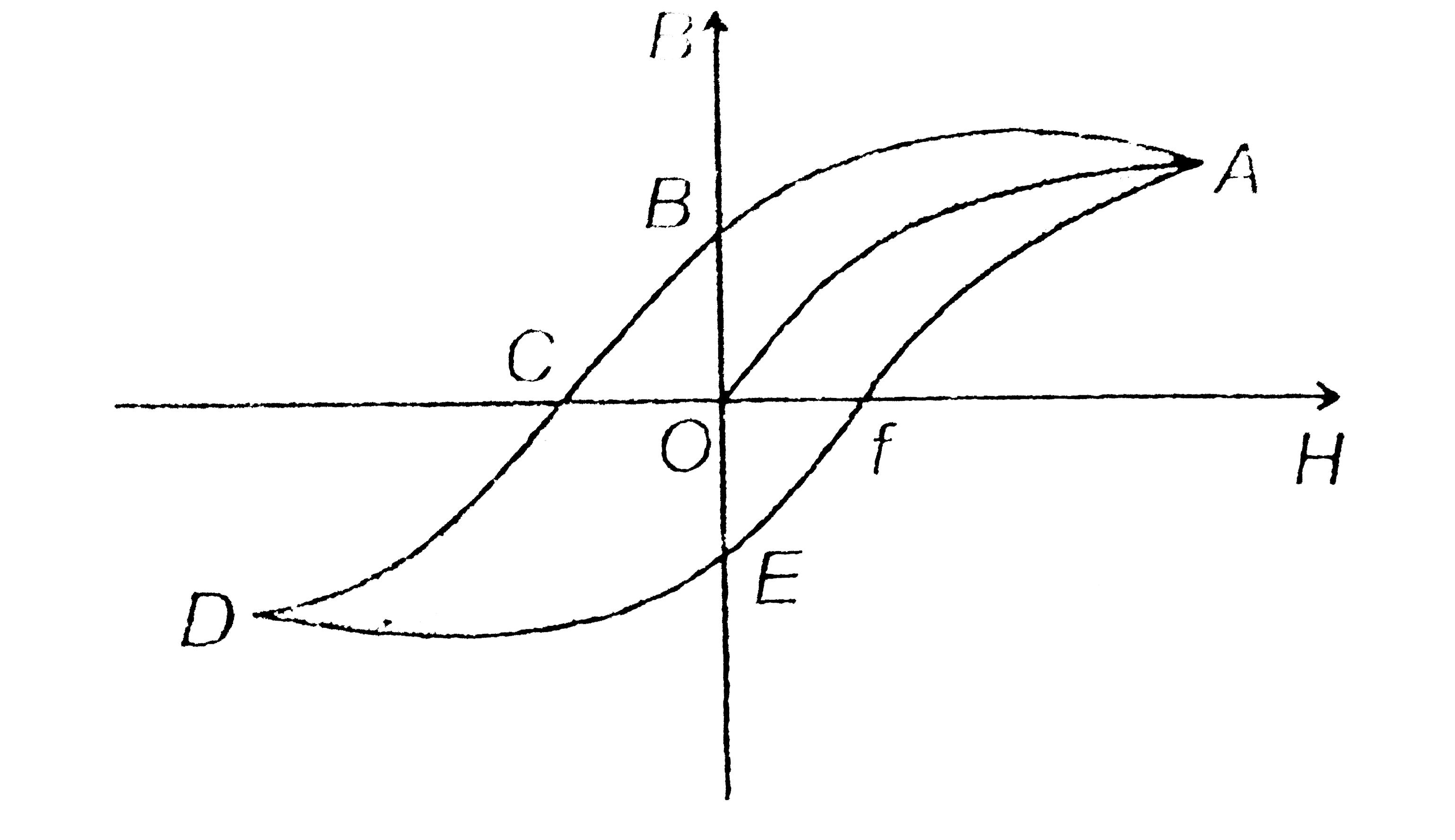
Energy loss
Energy loss per unit area
Energy loss per unit volume
Power loss per unit area
The correct Answer is:C
Step by step video & image solution for Area under this given curve gives by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section - B Objective Type Questions (One option is correct)
30 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Assignment Section- C Linked Comprehension Type Questions
3 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Try Yourself
53 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
Find the area under the given curves and given lines:(i) y=x2,x=1,x=2and x-axis(ii) y=x4, x=1,x=5and x-axis
View SolutionArea under speed-time curve gives
View SolutionThe area under force time curve gives
View SolutionDraw a rough sketch of the curve y=√x−1 in the interval [1, 5] and find the area under the given curve and between the lines x = 1 and x = 5.
View Solution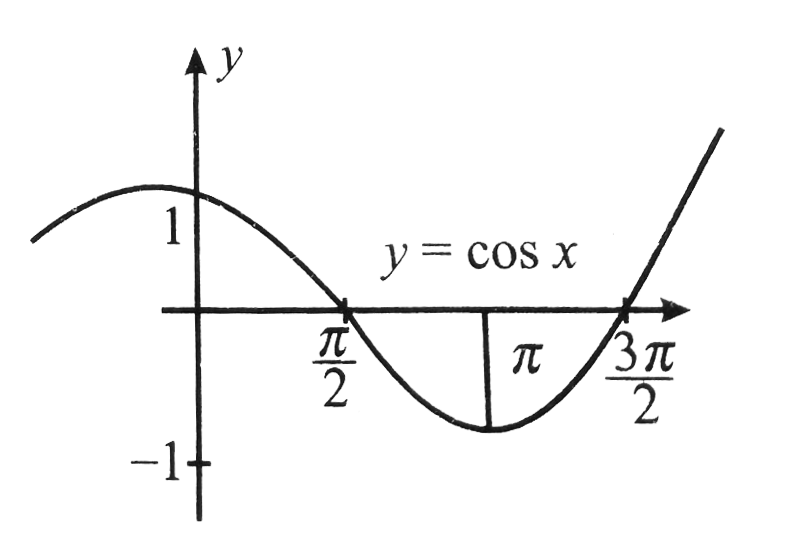
Find the area under the curve y=cosx over the interval
(a) [0,π2]
(b) [0,π]
View SolutionFind the area under the curve y=sin2x+cos2x between the ordinates x = 0, x=π4
View SolutionCompare the areas under the curves y=cos2x and y=sin2x between x=0 and x=π.
View SolutionShow that the areas under the curves y=sinx and y=sin2x between x=0 and x=π3 are in the ratio 2:3.
View SolutionFind the area under the curve y=(x2+2)2+2x between the ordinates x =0 and x=2
View SolutionThe spectral emissive power Eλ for a body at temperature T1 is poltted againist the wavelenght and area under the curve is found to be 9A.At a different temperature T2 the area is found to be A then λ1/λ2=
 .
.
View Solution
