A gun mounted on the top of a moving truck t is aimed in the backward direction at an angle of 30° to the vertical. If the muzzle velocity of the bullet is 4ms−1 the value of speed of the truck that will make the bullet come of out vertically is
1ms−1
√32ms−1
0.5ms−1
2ms−1
The correct Answer is:D
To solve the problem, we need to analyze the motion of the bullet fired from the gun mounted on the truck. The bullet is aimed backward at an angle of 30° to the vertical, and we need to find the speed of the truck such that the bullet exits vertically.
1. Understand the Problem:
- The bullet is fired at an angle of 30° to the vertical.
- The muzzle velocity of the bullet is u=4m/s.
- We need to determine the speed of the truck vt such that the bullet exits vertically.
2. Break Down the Bullet's Velocity:
- The bullet's velocity can be resolved into two components:
- Vertical component: uy=ucos(30°)
- Horizontal component: ux=usin(30°)
3. Calculate the Components:
- Using cos(30°)=√32 and sin(30°)=12:
- uy=4cos(30°)=4×√32=2√3m/s
- ux=4sin(30°)=4×12=2m/s
4. Condition for Vertical Exit:
- For the bullet to exit vertically, the horizontal component of the bullet's velocity must be equal to the speed of the truck moving in the opposite direction.
- Therefore, we set:
vt=ux
5. Substituting the Values:
- From the previous calculation, we found ux=2m/s.
- Thus, the speed of the truck vt is:
vt=2m/s
Final Answer:
The speed of the truck that will make the bullet come out vertically is 2m/s.
---
- The bullet is fired at an angle of 30° to the vertical.
- The muzzle velocity of the bullet is u=4m/s.
- We need to determine the speed of the truck vt such that the bullet exits vertically.
- The bullet's velocity can be resolved into two components:
- Vertical component: uy=ucos(30°)
- Horizontal component: ux=usin(30°)
- Using cos(30°)=√32 and sin(30°)=12:
- uy=4cos(30°)=4×√32=2√3m/s
- ux=4sin(30°)=4×12=2m/s
- For the bullet to exit vertically, the horizontal component of the bullet's velocity must be equal to the speed of the truck moving in the opposite direction.
- Therefore, we set:
vt=ux
- From the previous calculation, we found ux=2m/s.
- Thus, the speed of the truck vt is:
vt=2m/s
The speed of the truck that will make the bullet come out vertically is 2m/s.
Similar Questions
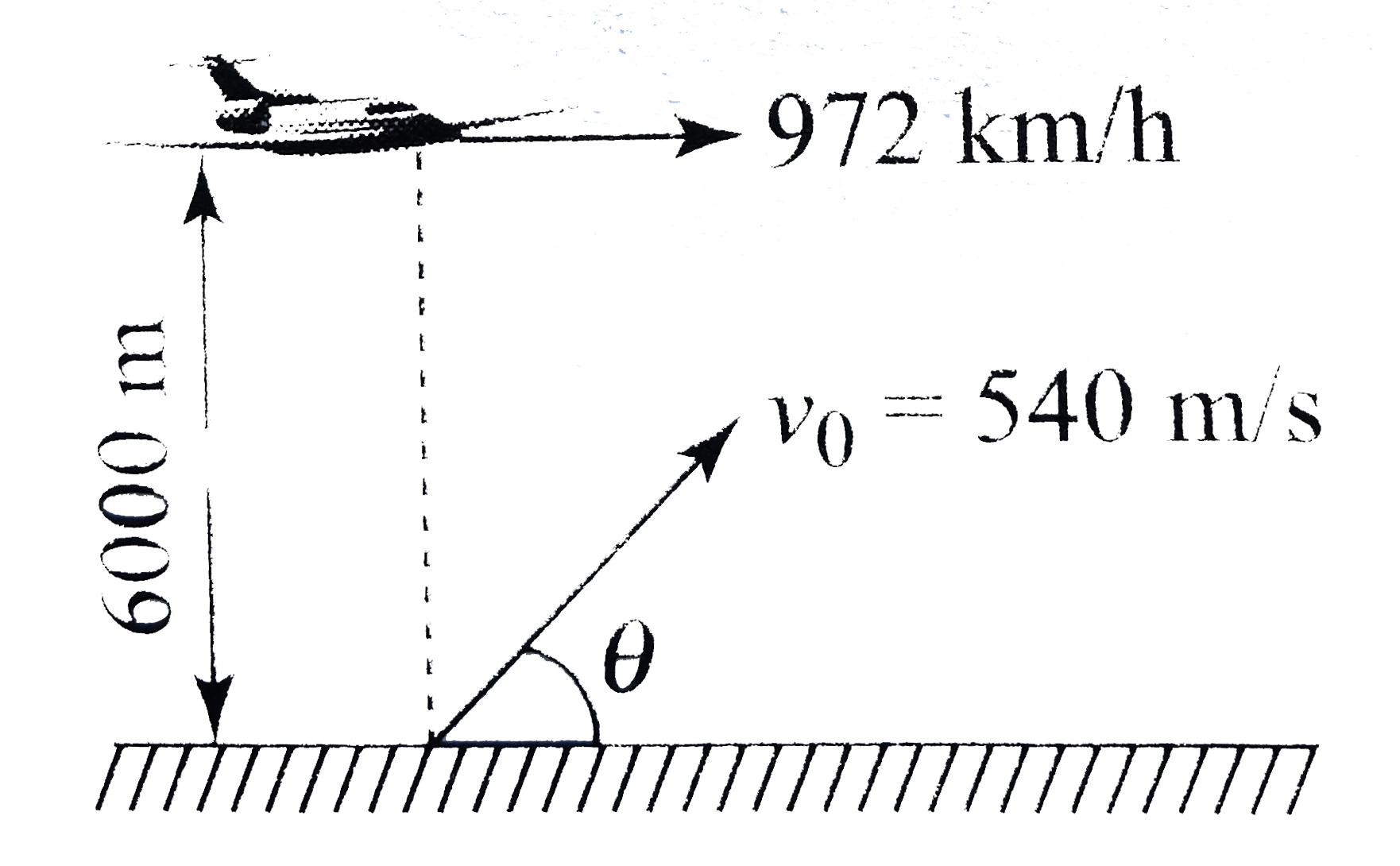
An aircraft moving with a speed of 1000 km/h is at a heirgh of 6000 m, just overhead of an anti-aircraft gun. If the muzzle velocity of the gun is 540 m/s, the firing angle θ for the bullet to hit the aircraft should be
View SolutionA football is kicked at an angle of 30∘ with the vertical, so if the horizontal component of its velocity is 20ms−1, determine its maximum height.
View Solution
Knowledge Check
A police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .A95ms−1B105ms−1C115ms−1D125ms−1
.A95ms−1B105ms−1C115ms−1D125ms−1
A police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .
.
View SolutionA police van moving on a highway with a speed of 30kmh−1 Fires a bullet at a thief's car speeding away in a same direction with a speed of 192kmh−1. If the muzzle speed of the buller is 150ms−1, with what speed does the bullet hit thief's car? .
 .
.
View SolutionA machine gun is mounted on the top of a tower of height h. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ? The muzzle speed of bullet is 150ms−1. Take g=10ms−2.
View SolutionA machine gun is mounted on an armored car moving with a speed of 20ms−1. The gun point against the direction of motion of car. The muzzle speed of bullet is equal to speed of sound in air i.e., 340ms−1. The time difference between bullet actually reaching and sound of firing reaching at a target 544m away from car at the instant of firing is reaching at a target 544m away from car at the instant of firing is

View SolutionA body is projected with velocity 24 ms−1 making an angle 30° with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1 )
View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View SolutionIt is raining at a speed of 5ms−1 at an angle 37∘ to vertical, towards east. A man is moving to west with a velocity of 5ms−1. The angle with the vertical at which he has to hold the umbrella to protect himself from rain is
View Solution
