A block of weight 100N is lying on a rough horizontal surface. If coefficient of friction 1/√3. The least possible force that can move the block is
100√3
100√3
50√3
50N
The correct Answer is:D
To solve the problem, we need to find the least possible force required to move a block resting on a rough horizontal surface. The weight of the block and the coefficient of friction are given. Let's go through the solution step by step.
Step 1: Understand the given data
- Weight of the block (W) = 100 N
- Coefficient of friction (μ) = 1√3
Step 2: Identify the forces acting on the block
The forces acting on the block include:
- The weight of the block acting downwards (100 N).
- The normal force (N) acting upwards, which is equal to the weight of the block since it is on a horizontal surface.
- The frictional force (f) acting opposite to the direction of the applied force.
Step 3: Calculate the normal force
Since the block is resting on a horizontal surface and there are no vertical forces acting other than weight and normal force, we have:
N=W=100N
Step 4: Calculate the frictional force
The frictional force can be calculated using the formula:
f=μ⋅N
Substituting the known values:
f=1√3⋅100
f=100√3N
Step 5: Determine the least force required to move the block
To move the block, the applied force (F) must be greater than or equal to the frictional force. Therefore, the least possible force required to move the block is:
F≥f
F≥100√3N
Conclusion
The least possible force that can move the block is:
F=100√3N
- Weight of the block (W) = 100 N
- Coefficient of friction (μ) = 1√3
The forces acting on the block include:
- The weight of the block acting downwards (100 N).
- The normal force (N) acting upwards, which is equal to the weight of the block since it is on a horizontal surface.
- The frictional force (f) acting opposite to the direction of the applied force.
Since the block is resting on a horizontal surface and there are no vertical forces acting other than weight and normal force, we have:
N=W=100N
The frictional force can be calculated using the formula:
f=μ⋅N
Substituting the known values:
f=1√3⋅100
f=100√3N
To move the block, the applied force (F) must be greater than or equal to the frictional force. Therefore, the least possible force required to move the block is:
F≥f
F≥100√3N
The least possible force that can move the block is:
F=100√3N
Similar Questions
A block of mass 5kg is placed on a rough horizontal plane whose coefficient of friction is 0.3. Find the least horizontal force needed to move the block along the plane and the resultant of normal reaction and the force applied.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA block of mass 10 kg is placed on a rough horizontal surface of coefficient of friction 0.1. A pulling force of 100 N acts on it at 37∘ with the horizontal. The frictional force acting on the body is ..... N.
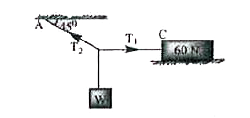
View SolutionIn the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5. The minimum weight of the block does not slip on the surface is (x×10)N. The value of x is
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution