A plane longitudinal wave of angular frequency ω=1000 rad/s is travelling along positive x direction in a homogeneous gaseous medium of density d=1kgm−3 . Intensity of wave is I=10−10W.m−2 and maximum pressure change is (ΔP)m=2×10−4Nm−2 . Assuming at x = 0, initial phase of medium particles to be zero
Amplitude of the travelling wave is
(a) 10−6m
(b) 10−7m
(c) 10−9m
(d) 2×10−8m
10−6m
10−7m
109m
2×10−8m
The correct Answer is:C
To find the amplitude of the traveling wave, we will use the given information and relevant equations step by step.
Step 1: Write down the known values
We have the following values from the problem:
- Angular frequency, ω=1000rad/s
- Density, d=1kg/m3
- Intensity, I=10−10W/m2
- Maximum pressure change, ΔPm=2×10−4N/m2
Step 2: Use the intensity formula
The intensity I of a longitudinal wave can be expressed as:
I=12ρvω2A2
where A is the amplitude, ρ is the density, and v is the velocity of the wave.
Step 3: Express velocity in terms of pressure change
For a longitudinal wave, the maximum pressure change ΔPm can be related to the amplitude and angular frequency as follows:
ΔPm=ρvAω
From this, we can express vA:
vA=ΔPmρω
Step 4: Substitute known values
Substituting the known values into the equation for vA:
vA=2×10−41×1000=2×10−7m2/s
Step 5: Use the intensity equation
Now, we can substitute vA back into the intensity equation. First, we need to express v in terms of A:
From the intensity equation:
I=12ρvω2A2
We can express v as:
v=I12ρω2A2
Step 6: Substitute vA into the intensity equation
Using the relation vA=2×10−7:
I=12ρ(2×10−7A)ω2A2
This simplifies to:
I=ρω2A×10−7
Step 7: Solve for amplitude A
Now we can rearrange the equation to solve for A:
A=Iρω2×10−7
Substituting the values:
A=10−101×(1000)2×10−7=10−10106×10−7=10−1010−1=10−9m
Conclusion
Thus, the amplitude of the traveling wave is:
10−9m
This corresponds to option (c).
---
We have the following values from the problem:
- Angular frequency, ω=1000rad/s
- Density, d=1kg/m3
- Intensity, I=10−10W/m2
- Maximum pressure change, ΔPm=2×10−4N/m2
The intensity I of a longitudinal wave can be expressed as:
I=12ρvω2A2
where A is the amplitude, ρ is the density, and v is the velocity of the wave.
For a longitudinal wave, the maximum pressure change ΔPm can be related to the amplitude and angular frequency as follows:
ΔPm=ρvAω
From this, we can express vA:
vA=ΔPmρω
Substituting the known values into the equation for vA:
vA=2×10−41×1000=2×10−7m2/s
Now, we can substitute vA back into the intensity equation. First, we need to express v in terms of A:
From the intensity equation:
I=12ρvω2A2
We can express v as:
v=I12ρω2A2
Using the relation vA=2×10−7:
I=12ρ(2×10−7A)ω2A2
This simplifies to:
I=ρω2A×10−7
Now we can rearrange the equation to solve for A:
A=Iρω2×10−7
Substituting the values:
A=10−101×(1000)2×10−7=10−10106×10−7=10−1010−1=10−9m
Thus, the amplitude of the traveling wave is:
10−9m
This corresponds to option (c).
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
1 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-V (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
8 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
1 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
A plane longitudinal wave of angular frequency ω=1000 rad Is is travelling along positive x direction in a homogeneous gaseous medium of density d=1kgm−3 . Intensity of wave is I=10−10W.m−2 and maximum pressure change is (ΔP)m=2×10−4Nm−2 . Assuming at x = 0, initial phase of medium particles to be zero
Velocity of the wave is
View SolutionA plane longitudinal wave having angular frequency ω = 500 rad /sec is travelling in positive x-direction in a medium of density ρ =1 kg/m and bulk modulus 4×104N/m2 . The loudness at a point in the medium is observed to be 20 dB. Assuming at x = 0 initial phase of the medium particles to be zero, find the equation of the wave
View SolutionTwo waves of equal amplitude 1m and equal frequency travel in the opposite direction in a medium. The magnitude of amplitude of the resultant wave may not be
View SolutionTwo waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
View SolutionIf sound wave of frequency 500Hz and wavelength 0.66m is travelling in a medium. Calculate the velocity of the wave in the medium.
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 360m/sec if λ=60m, then correct exression for the wave is
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 360m/sec if λ=60m, then correct exression for the wave is
View SolutionThe intensity of a wave emitted from a small source at a distance 10 m is 20×10−3Wm−2. What is the intensity at a distance 100 m ?
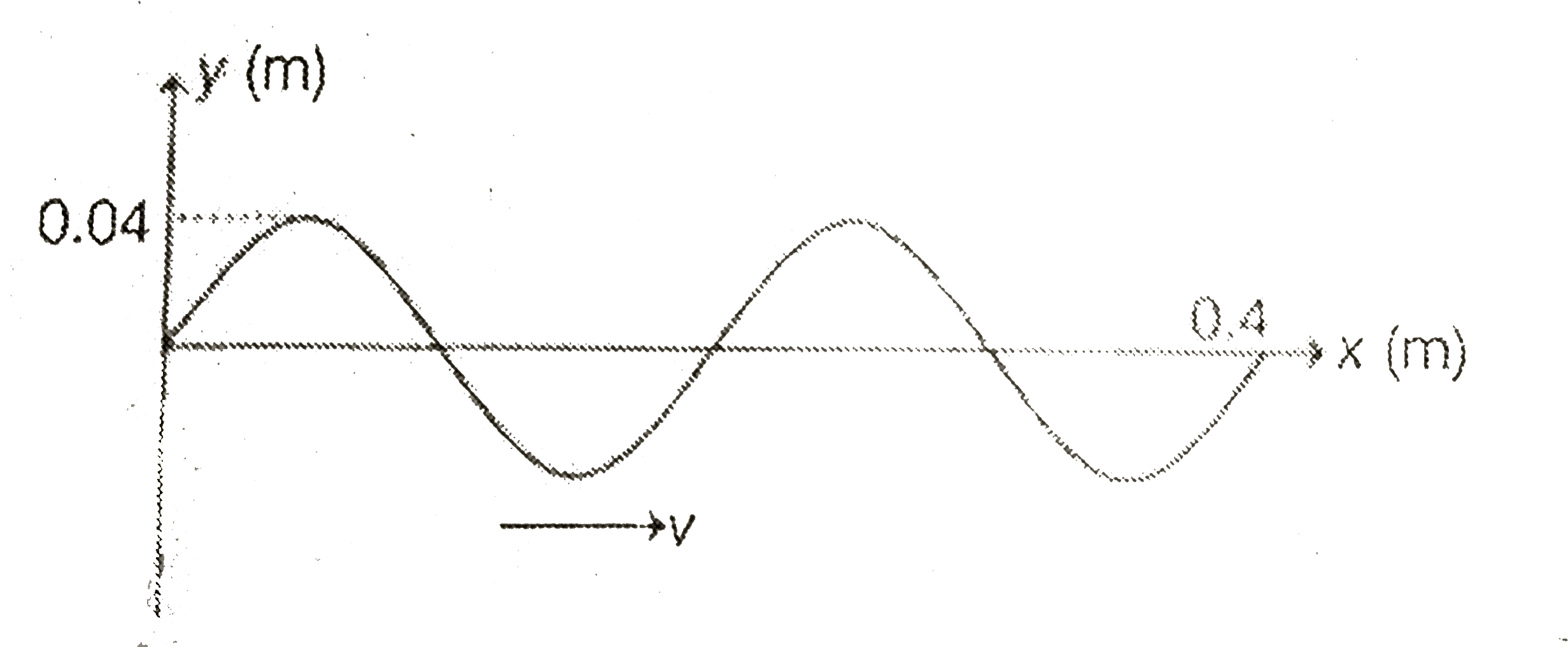
View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Frequency of the wave is

View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Equation of the wave is (in SI unit)
View Solution
