If I1,I2andI3 are wave lengths of the waves giving resonance with fundamental, first and second over tones of closed organ pipe. The ratio of wavelengths I1:I2:I3 is.....
1:2:3
1:13:15
1:3:5
5:3:1
The correct Answer is:B
To find the ratio of wavelengths I1:I2:I3 for the fundamental frequency and the first and second overtones of a closed organ pipe, we can follow these steps:
Step 1: Understand the relationship between frequency and wavelength
The relationship between frequency f, wavelength λ, and wave speed v is given by the equation:
v=f⋅λ
From this, we can express wavelength as:
λ=vf
Step 2: Identify the frequencies for the fundamental and overtones
For a closed organ pipe, the frequencies of the fundamental frequency and the overtones can be expressed as:
- Fundamental frequency (n=1):
f1=1⋅v4L
- First overtone (n=2):
f2=3⋅v4L
- Second overtone (n=3):
f3=5⋅v4L
Where L is the length of the pipe.
Step 3: Write the ratios of frequencies
Now we can write the ratio of frequencies:
f1:f2:f3=1:3:5
Step 4: Find the ratios of wavelengths
Using the relationship λ=vf, we can find the wavelengths:
- Wavelength for fundamental frequency (I1):
I1=vf1=v1⋅v4L=4L
- Wavelength for first overtone (I2):
I2=vf2=v3⋅v4L=4L3
- Wavelength for second overtone (I3):
I3=vf3=v5⋅v4L=4L5
Step 5: Write the ratio of wavelengths
Now we can write the ratio of wavelengths:
I1:I2:I3=4L:4L3:4L5
Step 6: Simplify the ratio
To simplify this ratio, we can eliminate 4L from each term:
1:13:15
To express this in whole numbers, we can find a common denominator, which is 15:
1⋅15:13⋅15:15⋅15=15:5:3
Thus, the final ratio of wavelengths is:
I1:I2:I3=15:5:3
Final Answer
The ratio of wavelengths I1:I2:I3 is 15:5:3.
The relationship between frequency f, wavelength λ, and wave speed v is given by the equation:
v=f⋅λ
From this, we can express wavelength as:
λ=vf
For a closed organ pipe, the frequencies of the fundamental frequency and the overtones can be expressed as:
- Fundamental frequency (n=1):
f1=1⋅v4L
- First overtone (n=2):
f2=3⋅v4L
- Second overtone (n=3):
f3=5⋅v4L
Where L is the length of the pipe.
Now we can write the ratio of frequencies:
f1:f2:f3=1:3:5
Using the relationship λ=vf, we can find the wavelengths:
- Wavelength for fundamental frequency (I1):
I1=vf1=v1⋅v4L=4L
- Wavelength for first overtone (I2):
I2=vf2=v3⋅v4L=4L3
- Wavelength for second overtone (I3):
I3=vf3=v5⋅v4L=4L5
Now we can write the ratio of wavelengths:
I1:I2:I3=4L:4L3:4L5
To simplify this ratio, we can eliminate 4L from each term:
1:13:15
To express this in whole numbers, we can find a common denominator, which is 15:
1⋅15:13⋅15:15⋅15=15:5:3
I1:I2:I3=15:5:3
The ratio of wavelengths I1:I2:I3 is 15:5:3.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-V (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
11 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-V (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
2 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
1 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
View SolutionIf λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View Solution
Knowledge Check
In the circuit shown, the value of currents I1,I2andI3 are
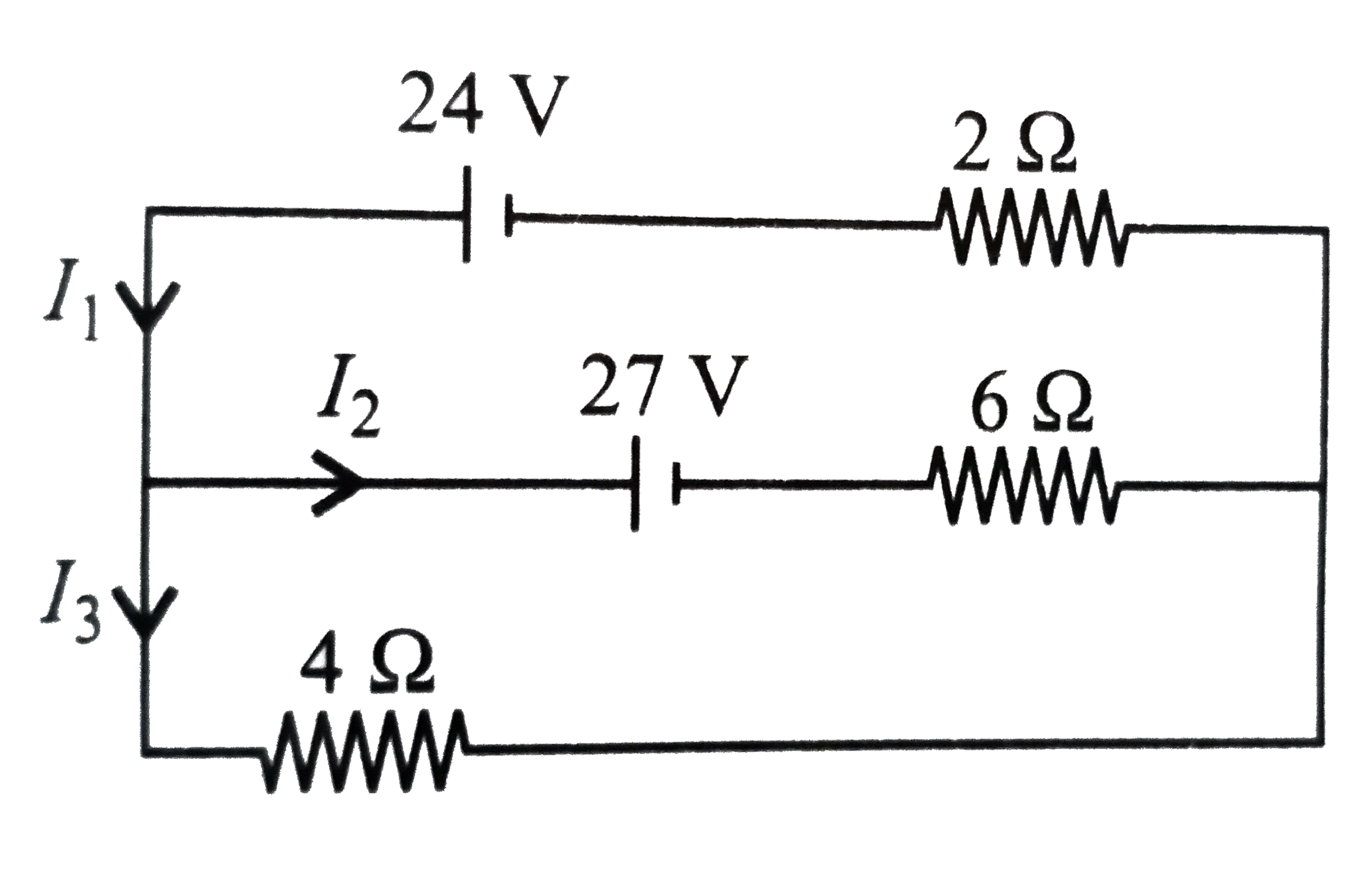 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
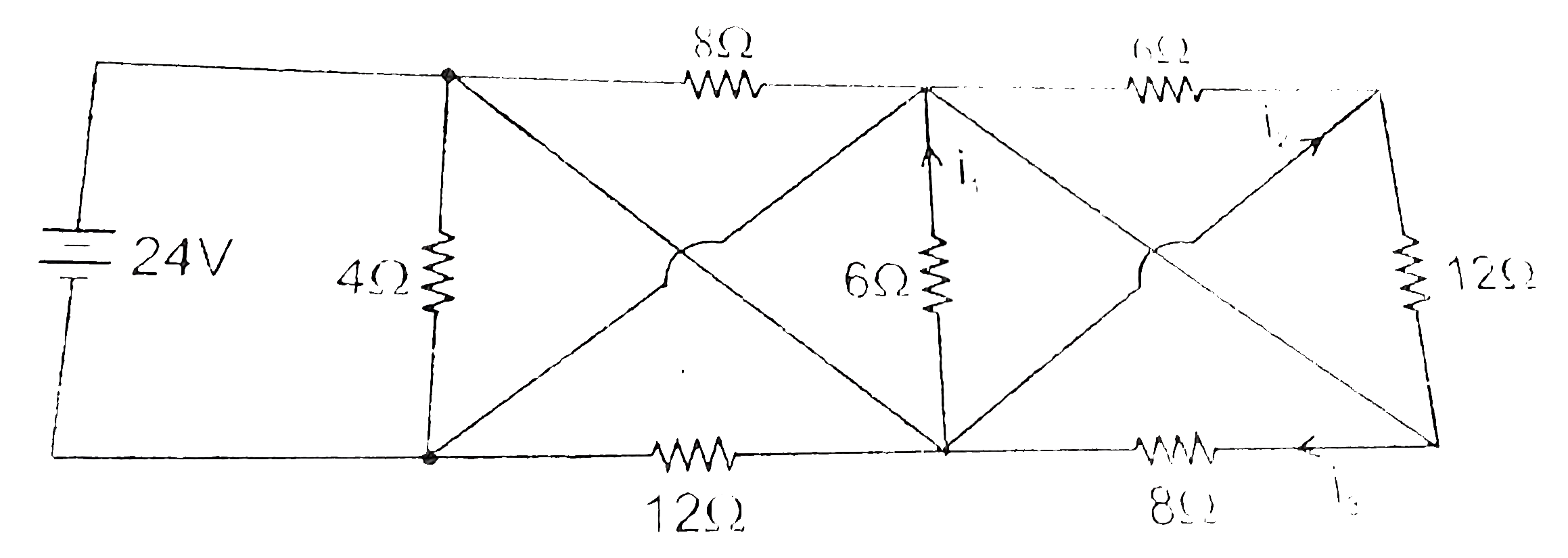
Calculate ratio of i1 and (i2+i3)
View SolutionDependence of disturbances due to two waves on time is shown in the figure. The ratio of their intensities I1/I2 will be
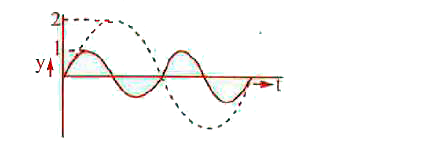
View SolutionDepedence is disturbances due to two waves on time is shown in the figure, The ratio of their intensities I1/I2 be :-
_E01_012_Q01.png) .
.
View SolutionShow that an organ pipe of length 2l open at both ends has the same fundamental frequency as another pipe of length I closed at one end.
View SolutionIn the circuit shown in figure ,find the ratio of currents i1/i2.

View SolutionIf I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is
View SolutionIf I1,I2,I3 are the centers of escribed circles of ΔABC, show that the area of ΔI1I2I3 is (abc)/(2r)
View Solution
