A ray of light entering from air to glas (μ=1.5) is partly reflected and partly refracted. lf the reflected and refracted rays are at right angles to each other, the angle of refraction is
sin−1(√213)
sin−1(√213)
sin−1(2√13)
sin−1(3√13)
The correct Answer is:C
To solve the problem, we need to find the angle of refraction when a ray of light enters from air into glass, given that the reflected and refracted rays are at right angles to each other.
1. Understanding the Geometry:
- When a ray of light travels from air (refractive index μ1=1) into glass (refractive index μ2=1.5), it undergoes partial reflection and refraction.
- Let i be the angle of incidence, r be the angle of refraction, and r′ be the angle of reflection. According to the law of reflection, i=r′.
2. Setting Up the Angles:
- The problem states that the reflected and refracted rays are at right angles to each other. Therefore, we can write:
r′+r=90∘
- This implies:
r=90∘−r′
3. Using the Law of Reflection:
- Since r′=i, we can substitute this into the equation:
r=90∘−i
4. Applying Snell's Law:
- Snell's law states:
μ1sin(i)=μ2sin(r)
- Substituting the values of refractive indices:
1⋅sin(i)=1.5⋅sin(r)
5. Substituting for r:
- From step 3, we know r=90∘−i. Therefore:
sin(r)=sin(90∘−i)=cos(i)
- Now substituting this into Snell's law gives:
sin(i)=1.5⋅cos(i)
6. Using the Identity:
- We can use the identity sin(i)=√1−cos2(i):
√1−cos2(i)=1.5⋅cos(i)
7. Squaring Both Sides:
- Squaring both sides:
1−cos2(i)=2.25⋅cos2(i)
- Rearranging gives:
1=3.25⋅cos2(i)
- Thus:
cos2(i)=13.25=413
8. Finding sin(i):
- Now, using sin2(i)+cos2(i)=1:
sin2(i)=1−413=913
- Therefore:
sin(i)=3√13
9. Finding sin(r):
- Now substituting back into the equation sin(i)=1.5⋅cos(i):
sin(r)=11.5⋅sin(i)=23⋅3√13=2√13
10. Calculating the Angle of Refraction:
- Finally, we find the angle of refraction r:
r=sin−1(2√13)
Final Answer:
The angle of refraction r is sin−1(2√13).
---
- When a ray of light travels from air (refractive index μ1=1) into glass (refractive index μ2=1.5), it undergoes partial reflection and refraction.
- Let i be the angle of incidence, r be the angle of refraction, and r′ be the angle of reflection. According to the law of reflection, i=r′.
- The problem states that the reflected and refracted rays are at right angles to each other. Therefore, we can write:
r′+r=90∘
- This implies:
r=90∘−r′
- Since r′=i, we can substitute this into the equation:
r=90∘−i
- Snell's law states:
μ1sin(i)=μ2sin(r)
- Substituting the values of refractive indices:
1⋅sin(i)=1.5⋅sin(r)
- From step 3, we know r=90∘−i. Therefore:
sin(r)=sin(90∘−i)=cos(i)
- Now substituting this into Snell's law gives:
sin(i)=1.5⋅cos(i)
- We can use the identity sin(i)=√1−cos2(i):
√1−cos2(i)=1.5⋅cos(i)
- Squaring both sides:
1−cos2(i)=2.25⋅cos2(i)
- Rearranging gives:
1=3.25⋅cos2(i)
- Thus:
cos2(i)=13.25=413
- Now, using sin2(i)+cos2(i)=1:
sin2(i)=1−413=913
- Therefore:
sin(i)=3√13
- Now substituting back into the equation sin(i)=1.5⋅cos(i):
sin(r)=11.5⋅sin(i)=23⋅3√13=2√13
- Finally, we find the angle of refraction r:
r=sin−1(2√13)
The angle of refraction r is sin−1(2√13).
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
9 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
If a ray of light in a denser medium strikes a rarer medium at an angle of incidence i, the angles of reflection and refraction are respectively, r and r' If the reflected and refraction rays are at right angles to each other, the critical angle for the given pair of media is
View SolutionA ray of light from a denser medium strikes a rare medium as shown in figure. The reflected and refracted rays make an angle of 90∘ with each other. The angles of reflection and refraction are r and r'. The critical angle would be

View Solution
Knowledge Check
A ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
A12B√32C32D√3
A beam of light is partially reflected and partially refracted from a surface. The angle between reflected and refracted light ray is 90∘. If the angle of refraction is 30∘, the angle of incidence is
View SolutionFigure shows a ray of light AO incident on a rectangular glass block PQRS, which is silvered at the surface RS. The ray is partily reflected and partly refracted.
(a) Draw the path of the reflected and refracted rays.
(b) Show at least two rays emerging from the surface PQ after reflection from the surface RS.
(c) How many images are formed in the above case ? Which image is the brightest ?
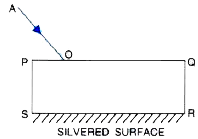
View SolutionA ray of light is incident at an angle i from denser to rare medium. The reflected and the refracted rays are mutually perpendicular. The angle of reflection and the angle of refraction are respectively r and r'. Then the critical angle will be:
View Solution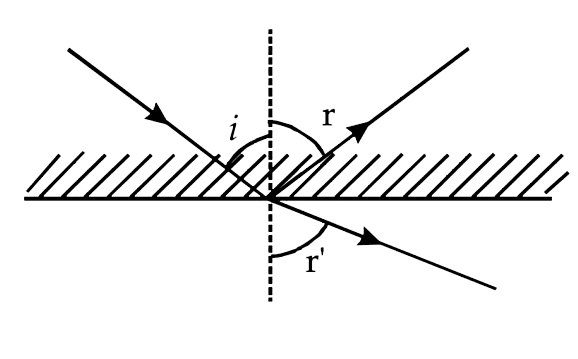
A ray of light from a denser medium strike a rarer medium at an angle of incidence I (see Fig). The reflected and refracted rays make as angle of 90degrees with each other. The angles of reflection and refraction are r and r The critical angle is
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

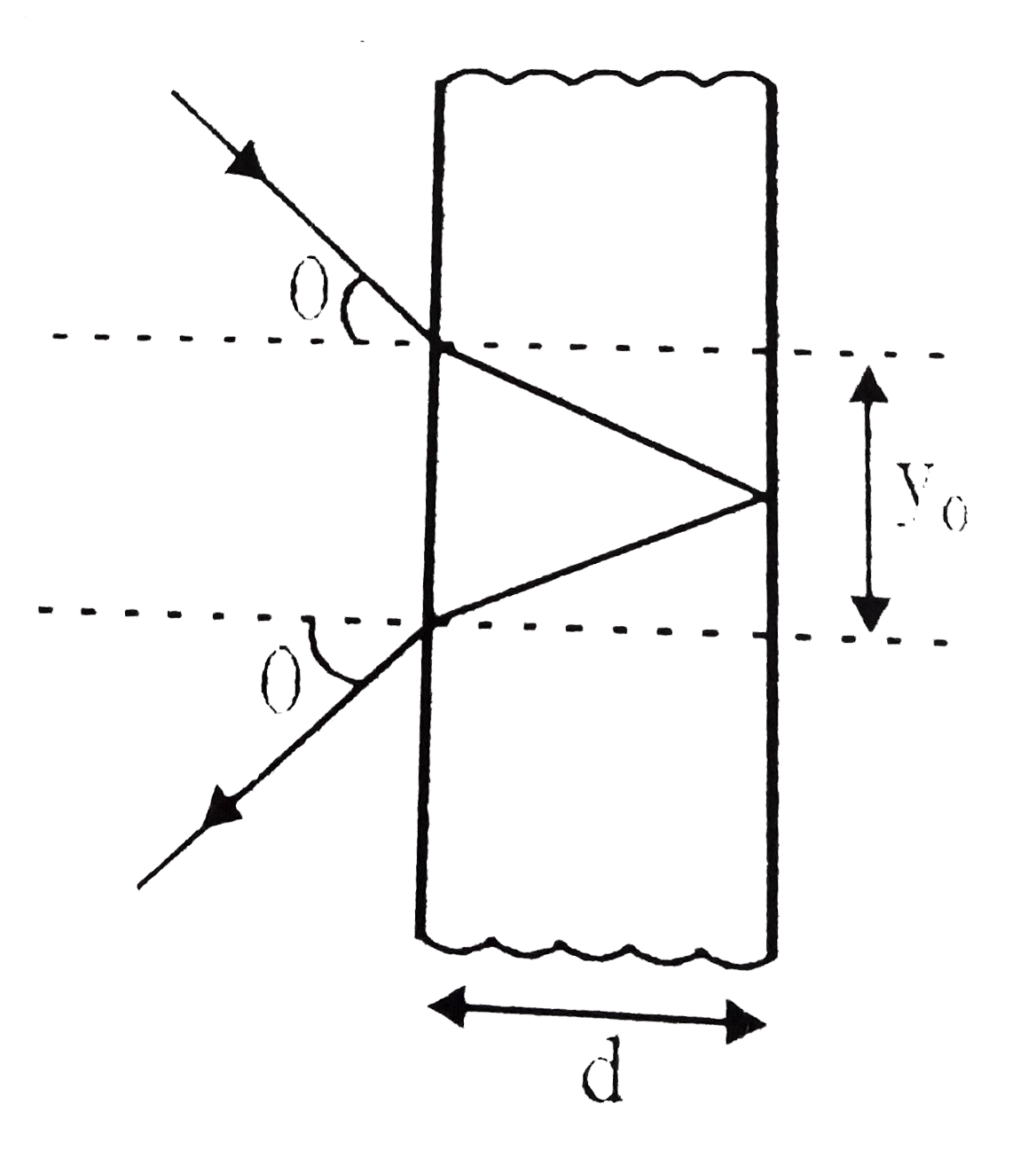
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
View SolutionStatement I: A light ray is incident on a glass slab. Some portion of it is reflected and some is refracted. Refracted and reflected rays are always perpendicular to each other.
Statement II: Angle of incidence is equal to angle of reflection.

View Solution
