A narrow beam of light after reflection by a plane mirror falls on a scale at a distance 100 cm from the mirror. When the mirror is rotated a little, the light spot moves through 2 cm. The angle through which the mirror is rotated is
0.02 rad
0.01 rad
200 rad
0.01/188 π rad
The correct Answer is:B
To solve the problem, we need to find the angle through which the mirror is rotated when a narrow beam of light reflects off a plane mirror and the light spot moves on a scale. Here’s a step-by-step solution:
Step 1: Understand the setup
- A plane mirror reflects a narrow beam of light.
- The distance from the mirror to the scale is given as 100 cm.
- When the mirror is rotated slightly, the light spot moves 2 cm on the scale.
Step 2: Identify the relationship between the arc and the angle
- The movement of the light spot on the scale can be treated as an arc of a circle, where the radius of the circle is the distance from the mirror to the scale (100 cm).
- The formula relating the angle (in radians) to the arc length and radius is:
θ=arcradius
Step 3: Substitute the known values
- Here, the arc length (the movement of the light spot) is 2 cm, and the radius is 100 cm.
- Substitute these values into the formula:
θ=2 cm100 cm=0.02 radians
Step 4: Relate the angle of mirror rotation to the angle of reflection
- For a plane mirror, the angle of reflection (r) is equal to the angle of incidence (i), and when the mirror is rotated by an angle θ, the angle of reflection changes by 2θ.
- Thus, if the angle of reflection is given by:
r=θ
Then, the angle through which the mirror is rotated (let’s denote it as α) is:
r=2α
Therefore, we can express the rotation angle as:
α=r2=0.02 radians2=0.01 radians
Step 5: Conclusion
- The angle through which the mirror is rotated is:
α=0.01 radians
Final Answer:
The angle through which the mirror is rotated is 0.01 radians.
---
- A plane mirror reflects a narrow beam of light.
- The distance from the mirror to the scale is given as 100 cm.
- When the mirror is rotated slightly, the light spot moves 2 cm on the scale.
- The movement of the light spot on the scale can be treated as an arc of a circle, where the radius of the circle is the distance from the mirror to the scale (100 cm).
- The formula relating the angle (in radians) to the arc length and radius is:
θ=arcradius
- Here, the arc length (the movement of the light spot) is 2 cm, and the radius is 100 cm.
- Substitute these values into the formula:
θ=2 cm100 cm=0.02 radians
- For a plane mirror, the angle of reflection (r) is equal to the angle of incidence (i), and when the mirror is rotated by an angle θ, the angle of reflection changes by 2θ.
- Thus, if the angle of reflection is given by:
r=θ
Then, the angle through which the mirror is rotated (let’s denote it as α) is:
r=2α
Therefore, we can express the rotation angle as:
α=r2=0.02 radians2=0.01 radians
- The angle through which the mirror is rotated is:
α=0.01 radians
The angle through which the mirror is rotated is 0.01 radians.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) INTEGER TYPE QUESTIONS)
2 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
When mirror is rotated through an angle θ, a reflected ray from it moves through an angle of
View SolutionA beam of light from a source L is incident normally on a plane mirror fixed at a certain distance x from the source. The beam is reflected back as a spot on a scale placed just above the source L. When the mirror is rotated through a small angle θ the spot of the light is found to move through a distance y on the scale. The angle θ is given by
View Solution
Knowledge Check
A ray of light after reflection from a mirror is known as
Areflected rayBnormalCincident rayDrefracted ray
A ray of light falls normally on a plane mirror. What is the angle of incidence ?
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
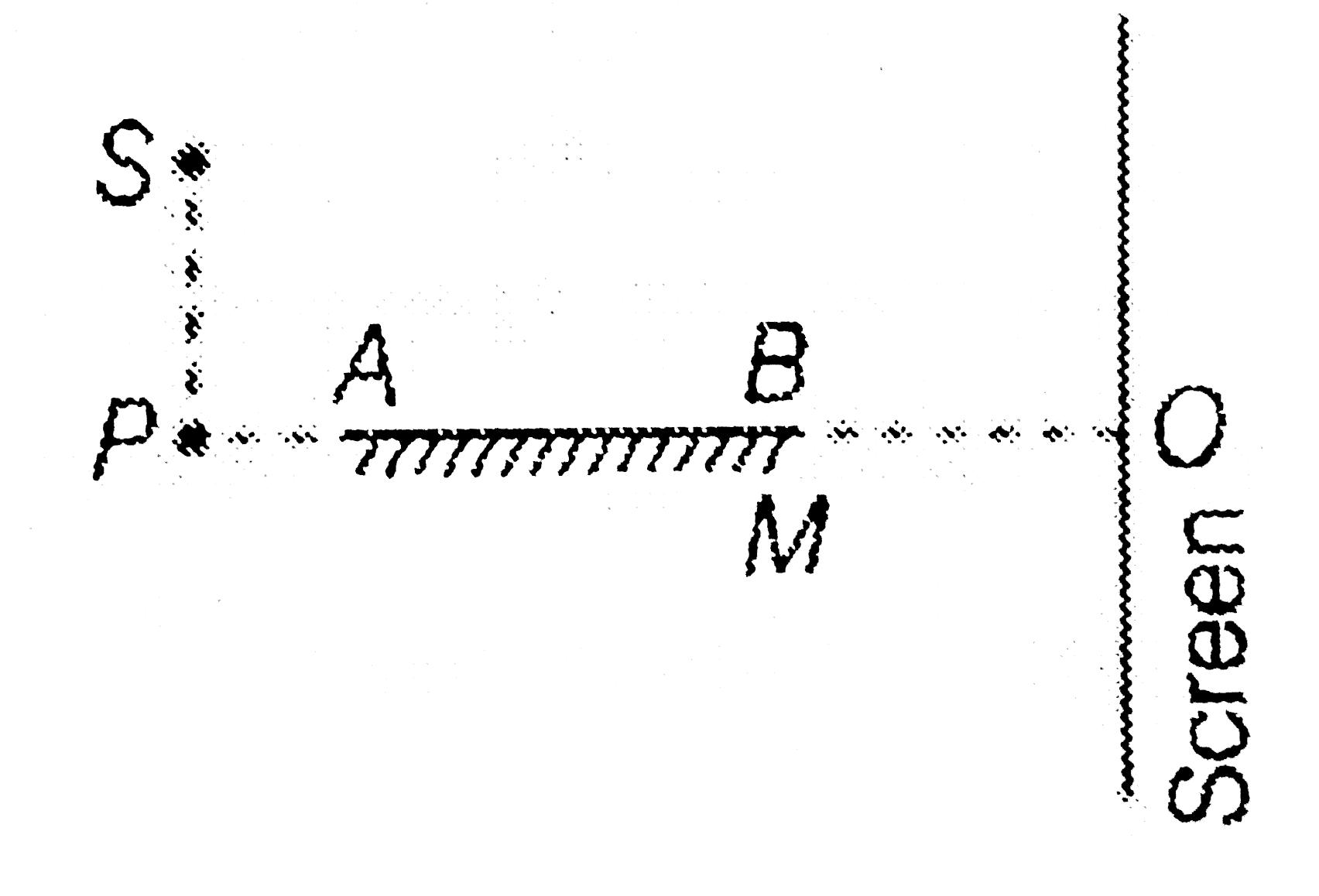
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionWhen a ray of light strikes a plane mirror along the normal, the angle of incidence is :
View SolutionA ray of light is incident on a plane mirror at an angle of incidence of 30∘. The deviation produced by the mirror is
View SolutionThe focus of a parabolic mirror is at a distance of 6 cm from its vertex. If the mirror is 20 cm deep, find the distance LM.
View SolutionWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
View Solution
