A thin convex lens made from crown glass has focal length . When it is measured in two different liquids having refractive indiced and , it has the focal length and respectively. The correct ralation between the focal lengths is
and the focal length is :
and both become negative
and becomes negative
To solve the problem, we will use the lens maker's formula for a thin lens in different media. The lens maker's formula is given by:
1f=(n−1)(1R1−1R2)
Where:
- f is the focal length of the lens,
- n is the refractive index of the lens material with respect to the medium,
- R1 and R2 are the radii of curvature of the lens surfaces.
For a thin convex lens made of crown glass with a refractive index μ=32, we will measure its focal length in two different liquids with refractive indices μ1=43 and μ2=53.
Step 1: Calculate the focal length in the first liquid
Using the lens maker's formula for the first liquid:
1f1=(32−43)(1R1−1R2)
To simplify 32−43:
32=96,43=86⟹32−43=96−86=16
Thus,
1f1=16(1R1−1R2)
Now, we can express f1:
f1=6(1R1−1R2)−1
Step 2: Calculate the focal length in the second liquid
Now, for the second liquid:
1f2=(32−53)(1R1−1R2)
To simplify 32−53:
32=96,53=106⟹32−53=96−106=−16
Thus,
1f2=−16(1R1−1R2)
Now, we can express f2:
f2=−6(1R1−1R2)−1
Step 3: Establish the relationship between f1 and f2
From the expressions we derived:
f1=6(1R1−1R2)−1
f2=−6(1R1−1R2)−1
This implies:
f2=−f1
Conclusion
The correct relation between the focal lengths is:
f2=−f1
- f is the focal length of the lens,
- n is the refractive index of the lens material with respect to the medium,
- R1 and R2 are the radii of curvature of the lens surfaces.
f2=−6(1R1−1R2)−1
Topper's Solved these Questions
Similar Questions
A thin convex lens which is made of glass (refractive index 1.5) has a focal length of 20 cm. It is now completely immersed in a transparent liquid having refractive index 1.75. Find the new focal length of the lens.
View SolutionTwo thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View SolutionA concave lens with unequal radii of curvature made of glass (μg=1.5) has a focal length of 40cm. If it is immersed in a liquid of refractive index μ1=2, then
View SolutionThe focal lengths of a lens are in the ratio 8:3 when it is immersed in two different liquids of refractive induces 1.6 and 1.2 respectively. The refractive index of the material of the lens is
View SolutionA double convex lens of focal length 30 cm is made of glass. When it is immersed in a liquid of refractive index 1.4, the focal length is found to be 126 cm. The critical angle between glass and the liquid is
View SolutionTwo thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionIn the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
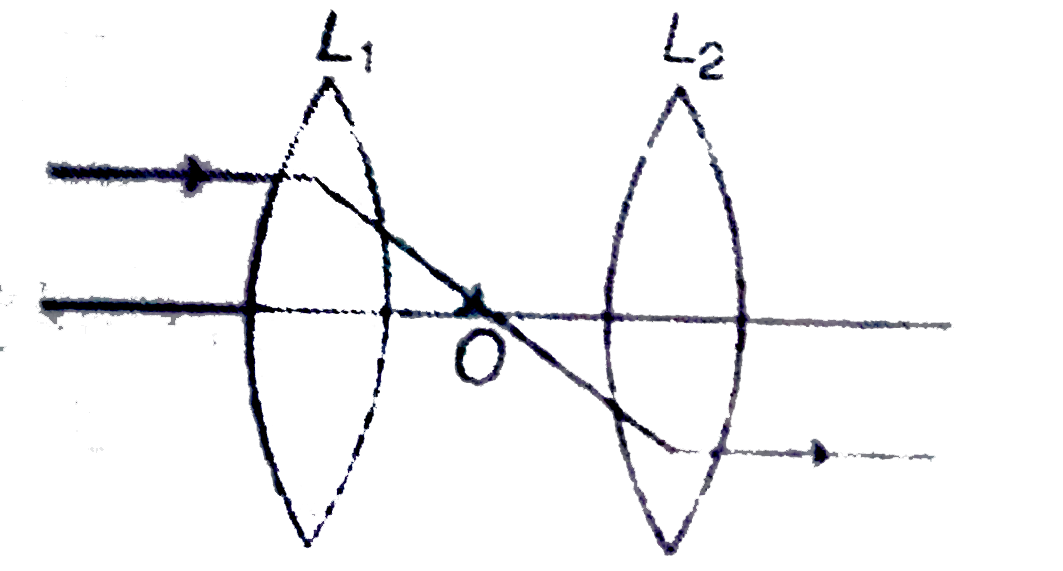
View SolutionA thin convex lens of refractive index 1.5cm has 20cm focal length in air. If the lens in completely immersed in a liquid of refractive index. 1.6, then its focal length will be
View SolutionA thin equiconvex lens (μ=3/2) of focal length 10cm is cut and separated and a material of refractive index 3 is filled between them. What is the focal length of the combination?

View SolutionA thin convergent glass lens (μg=1.5) has a power of +5.0D. When this lens is immersed in a liquid of refractive index μ1, it acts as a divergent lens of focal length 100cm. The value of μ1 is
View Solution
