A equilateral glass prism has a refractive index √2. A light ray is incident at 45∘ on one face. Total deviation of ray is n×15∘ where n is
The correct Answer is:2
To solve the problem, we need to calculate the total deviation of a light ray passing through an equilateral prism with a refractive index of √2 and an incident angle of 45∘.
1. Understand the Prism Geometry:
- An equilateral prism has angles of 60∘ each.
- The light ray is incident at 45∘ on one face of the prism.
2. Identify the Angles:
- Let i be the angle of incidence, which is 45∘.
- The angle of the prism A is 60∘.
- The angle of refraction r1 at the first face can be calculated using Snell's Law:
n1sin(i)=n2sin(r1)
where n1=1 (air) and n2=√2 (glass).
3. Calculate the Angle of Refraction:
- Using Snell's Law:
sin(45∘)=√2sin(r1)
1√2=√2sin(r1)
sin(r1)=12⟹r1=30∘
4. Determine the Angle of Refraction at the Second Face:
- The light ray travels inside the prism and hits the second face. The angle of incidence at the second face i2 can be found as:
i2=A−r1=60∘−30∘=30∘
- Now apply Snell's Law again at the second face:
√2sin(30∘)=1sin(r2)
√2⋅12=sin(r2)
sin(r2)=√22⟹r2=45∘
5. Calculate the Total Deviation:
- The total deviation δ can be calculated using:
δ=i+e−A
where e is the angle of emergence (which is equal to r2).
- Thus:
δ=45∘+45∘−60∘=30∘
6. Relate Total Deviation to Given Expression:
- The problem states that the total deviation is n×15∘.
- We have found that δ=30∘:
30∘=n×15∘
- Solving for n:
n=3015=2
Final Answer:
The value of n is 2.
- An equilateral prism has angles of 60∘ each.
- The light ray is incident at 45∘ on one face of the prism.
- Let i be the angle of incidence, which is 45∘.
- The angle of the prism A is 60∘.
- The angle of refraction r1 at the first face can be calculated using Snell's Law:
n1sin(i)=n2sin(r1)
where n1=1 (air) and n2=√2 (glass).
- Using Snell's Law:
sin(45∘)=√2sin(r1)
1√2=√2sin(r1)
sin(r1)=12⟹r1=30∘
- The light ray travels inside the prism and hits the second face. The angle of incidence at the second face i2 can be found as:
i2=A−r1=60∘−30∘=30∘
- Now apply Snell's Law again at the second face:
√2sin(30∘)=1sin(r2)
√2⋅12=sin(r2)
sin(r2)=√22⟹r2=45∘
- The total deviation δ can be calculated using:
δ=i+e−A
where e is the angle of emergence (which is equal to r2).
- Thus:
δ=45∘+45∘−60∘=30∘
- The problem states that the total deviation is n×15∘.
- We have found that δ=30∘:
30∘=n×15∘
- Solving for n:
n=3015=2
The value of n is 2.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-I (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
15 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-I (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
15 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (ADVANCED) (MATRIX MATCHING TYPE QUESTIOS)
1 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
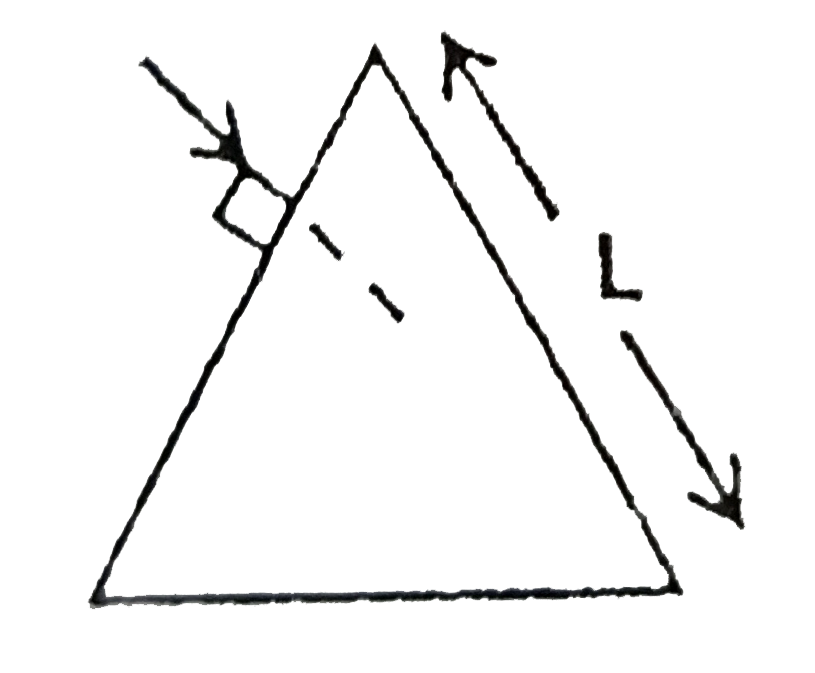
There is a equilateral prism of refractive index 3 on which a light ray is incident normally on one face as shown in the figure. Find the length of the path traveled by the light ray inside the prism.
View SolutionThe angle of a prism is 30∘. The rays incident at 60∘ on one refracting face suffer a deviation of 30∘. Then the angle of emergence is :
View SolutionThe angle of a prism is 30∘. The rays incident at 60∘ on one refracting face suffer a deviation of 30∘. Then the angle of emergence is :
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionAn isosceles glass prism has one of its faces silvered. A light ray is incident normally on the other face which is identical in size to the silvered face. The light ray is reflected twice on the same sized faces and emerges through the base of the prism perpendicularly. Find the minimum value of refractive index of the material of the prism.
View SolutionAn equilateral triangular prism is made of glass (μ=1.5). A ray of light is incident normally on one of the faces. The angle between the incident and emergent ray is
View SolutionA ray of light undergoes a deviation of 30∘ when incident on an equilateral prism of refractive index √2.
What is the angle subtended by the ray inside the prism with the base of the prism?

View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
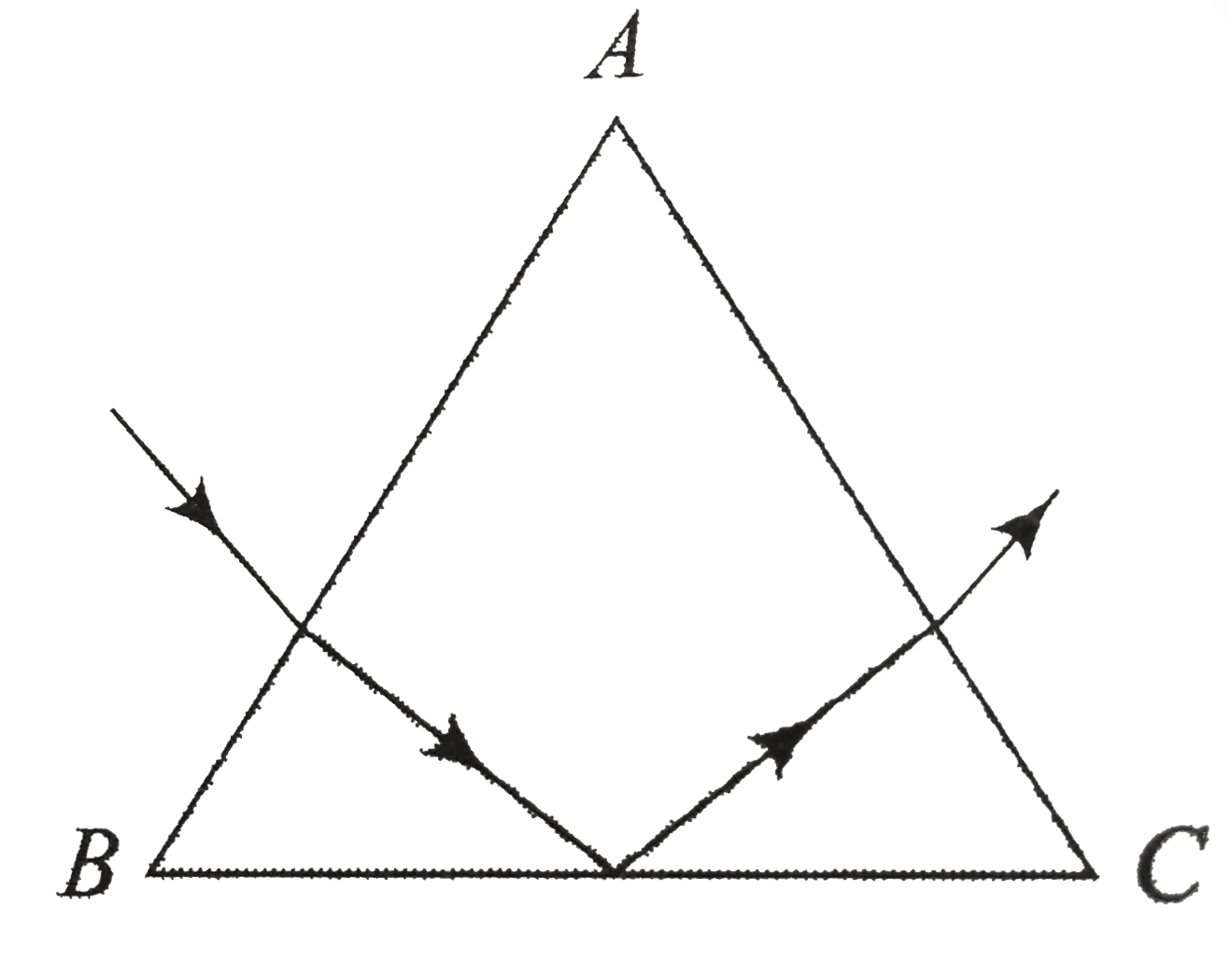
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionA glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
View Solution
