In a probability distribution of a random variable X , the sum of probabilities is always
a) 0
b) 1
c) 2
d) a non-negative integer
The correct Answer is:B
To solve the question regarding the sum of probabilities in a probability distribution of a random variable X, we can follow these steps:
1. Understanding Probability Distribution:
A probability distribution assigns probabilities to each possible outcome of a random variable. The random variable can take on various values, and each value has an associated probability.
Hint: Remember that a probability distribution is a way to describe how probabilities are assigned to different outcomes.
2. Definition of Probability:
The probability of an event is defined as the number of favorable outcomes divided by the total number of possible outcomes. For a random variable, this means that the probabilities assigned to all possible outcomes must add up to a specific value.
Hint: Recall the formula for probability: P(E)=Number of favorable outcomesTotal number of outcomes.
3. Total Probability:
In any probability distribution, the sum of the probabilities of all possible outcomes must equal 1. This is because the total probability represents the certainty that one of the possible outcomes will occur.
Hint: Think about the concept of certainty in probability; if you consider all possible outcomes, one of them must happen.
4. Example with Coin Toss:
Consider a simple example of tossing a fair coin. The possible outcomes are heads (H) and tails (T). The probabilities are:
- P(H)=12
- P(T)=12
When we add these probabilities together:
P(H)+P(T)=12+12=1
Hint: Use simple examples like coin tosses or dice rolls to visualize how probabilities add up.
5. Conclusion:
Therefore, in any probability distribution of a random variable X, the sum of all probabilities must always equal 1.
Final Answer: The correct answer to the question is 1.
A probability distribution assigns probabilities to each possible outcome of a random variable. The random variable can take on various values, and each value has an associated probability.
The probability of an event is defined as the number of favorable outcomes divided by the total number of possible outcomes. For a random variable, this means that the probabilities assigned to all possible outcomes must add up to a specific value.
In any probability distribution, the sum of the probabilities of all possible outcomes must equal 1. This is because the total probability represents the certainty that one of the possible outcomes will occur.
Consider a simple example of tossing a fair coin. The possible outcomes are heads (H) and tails (T). The probabilities are:
- P(H)=12
- P(T)=12
P(H)+P(T)=12+12=1
Therefore, in any probability distribution of a random variable X, the sum of all probabilities must always equal 1.
Similar Questions

is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionFind the probability distribution of the random variable x,which denotes the number of doublets in four throws of a pair of dice.Hence,find the mean of the number of doublets (X).
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
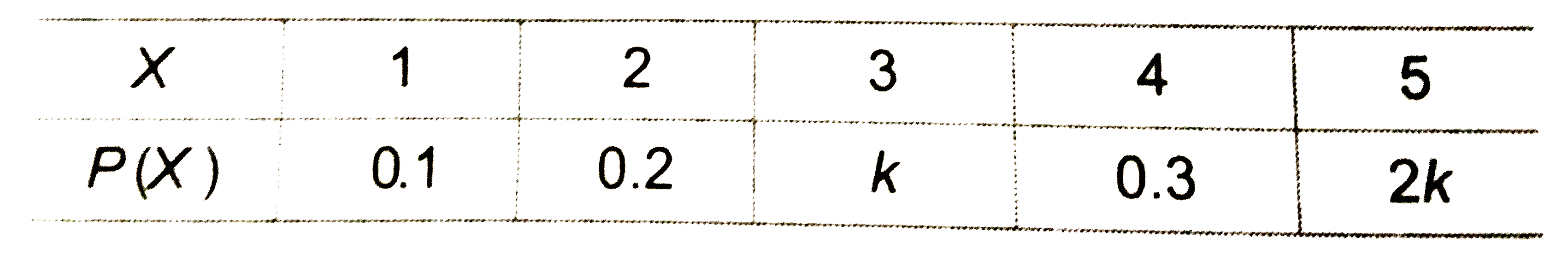
View SolutionA die is loaded in such a way that an even number is twice likely to occur as an odd number. If the die is tossed twice, find the probability distribution of the random variable X representing the perfect squares in the two tosses.
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability distribution of a random variable X is given below
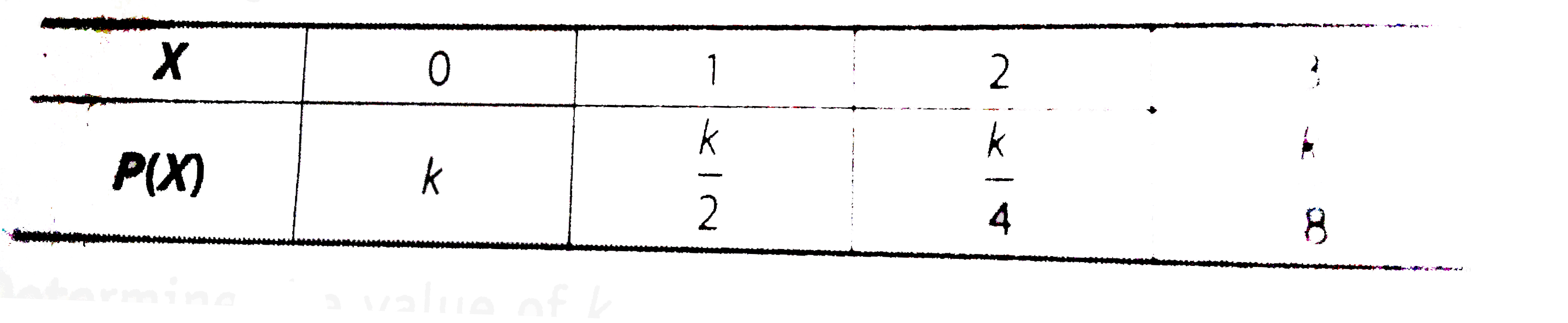
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View Solution
