The solution set of (x+1x)2−32(x−1x) =4 when x≠0 is
The correct Answer is:x = 2 or −1/2
To solve the equation (x+1x)2−32(x−1x)=4 where x≠0, we will follow these steps:
Step 1: Rewrite the equation
We start with the equation:
(x+1x)2−32(x−1x)=4
Step 2: Use the identity for squares
We know that:
(x+1x)2=(x−1x)2+4
This means we can rewrite the left side of our equation:
(x−1x)2+4−32(x−1x)=4
Step 3: Simplify the equation
Subtracting 4 from both sides gives:
(x−1x)2−32(x−1x)=0
Let t=x−1x. Then, we can rewrite the equation as:
t2−32t=0
Step 4: Factor the equation
Factoring out t gives:
t(t−32)=0
This gives us two possible solutions for t:
1. t=0
2. t=32
Step 5: Solve for x when t=0
If t=0:
x−1x=0⟹x2−1=0⟹(x−1)(x+1)=0
Thus, x=1 or x=−1.
Step 6: Solve for x when t=32
If t=32:
x−1x=32
Multiplying through by x gives:
x2−32x−1=0
To solve this quadratic equation, we can use the quadratic formula:
x=−b±√b2−4ac2a
where a=1,b=−32,c=−1:
x=32±√(−32)2−4⋅1⋅(−1)2⋅1
Calculating the discriminant:
(−32)2=94,4⋅1⋅(−1)=−4⟹−4=−164⟹94+164=254
Thus:
x=32±522
This gives us two solutions:
1. x=8/22=2
2. x=−2/22=−12
Step 7: Compile all solutions
The solutions we found are:
- From t=0: x=1,−1
- From t=32: x=2,−12
Thus, the complete solution set is:
{1,−1,2,−12}
We start with the equation:
(x+1x)2−32(x−1x)=4
We know that:
(x+1x)2=(x−1x)2+4
This means we can rewrite the left side of our equation:
(x−1x)2+4−32(x−1x)=4
Subtracting 4 from both sides gives:
(x−1x)2−32(x−1x)=0
Let t=x−1x. Then, we can rewrite the equation as:
t2−32t=0
Factoring out t gives:
t(t−32)=0
This gives us two possible solutions for t:
1. t=0
2. t=32
If t=0:
x−1x=0⟹x2−1=0⟹(x−1)(x+1)=0
Thus, x=1 or x=−1.
If t=32:
x−1x=32
Multiplying through by x gives:
x2−32x−1=0
To solve this quadratic equation, we can use the quadratic formula:
x=−b±√b2−4ac2a
where a=1,b=−32,c=−1:
x=32±√(−32)2−4⋅1⋅(−1)2⋅1
Calculating the discriminant:
(−32)2=94,4⋅1⋅(−1)=−4⟹−4=−164⟹94+164=254
Thus:
x=32±522
This gives us two solutions:
1. x=8/22=2
2. x=−2/22=−12
The solutions we found are:
- From t=0: x=1,−1
- From t=32: x=2,−12
{1,−1,2,−12}
Similar Questions
Knowledge Check
The solution set of |x−1|x>2 is
A0<x<13Bx<13Cx>13D13<x<1The solution set of 2x+13<3x−25x∈R on the number line is
A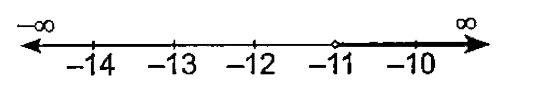 B
B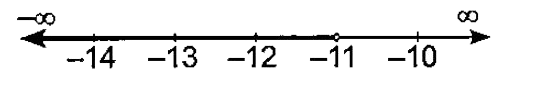 C
C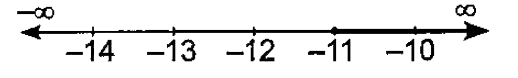 D
D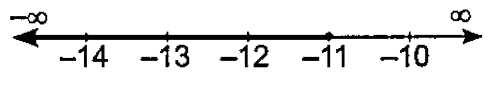
The solution set of x2+x+|x|+1<0, is
View SolutionThe solution set of (x2+x+1)(x2)log(x)(x+1)(x+9)<0 is
View SolutionSolve for x : 4(x−1x)2+8(x+1x)=29. x≠0.
View SolutionFind the solution set of (x−1)(x−2)2(x+4)(x+2)(x−3)≥0
View SolutionThe solution set of the inequation x2−3x+4x+1>1,x∈R, is
View SolutionThe solution set of the inequation ∣∣∣2x−1x−1∣∣∣>2, is
View Solution
