Solution set of 1x2−x+1≥4 is
x∈R
x∈(0,∞)
ϕ
None of these
The correct Answer is:C
To solve the inequality 1x2−x+1≥4, we can follow these steps:
Step 1: Rewrite the Inequality
We start with the inequality:
1x2−x+1≥4
To eliminate the fraction, we can multiply both sides by x2−x+1 (noting that x2−x+1>0 for all x):
1≥4(x2−x+1)
Step 2: Rearrange the Inequality
Now, we rearrange the inequality:
1≥4x2−4x+4
This can be rewritten as:
0≥4x2−4x+3
or
4x2−4x+3≤0
Step 3: Analyze the Quadratic
Next, we need to analyze the quadratic 4x2−4x+3. To do this, we will calculate the discriminant D:
D=b2−4ac=(−4)2−4⋅4⋅3=16−48=−32
Since the discriminant is negative (D<0), the quadratic 4x2−4x+3 does not intersect the x-axis and is always positive.
Step 4: Conclusion
Since 4x2−4x+3>0 for all x, the inequality 4x2−4x+3≤0 has no solutions. Therefore, the solution set for the original inequality is:
The solution set is ∅
We start with the inequality:
1x2−x+1≥4
To eliminate the fraction, we can multiply both sides by x2−x+1 (noting that x2−x+1>0 for all x):
1≥4(x2−x+1)
Now, we rearrange the inequality:
1≥4x2−4x+4
This can be rewritten as:
0≥4x2−4x+3
or
4x2−4x+3≤0
Next, we need to analyze the quadratic 4x2−4x+3. To do this, we will calculate the discriminant D:
D=b2−4ac=(−4)2−4⋅4⋅3=16−48=−32
Since the discriminant is negative (D<0), the quadratic 4x2−4x+3 does not intersect the x-axis and is always positive.
Since 4x2−4x+3>0 for all x, the inequality 4x2−4x+3≤0 has no solutions. Therefore, the solution set for the original inequality is:
The solution set is ∅
Topper's Solved these Questions
- QUADRATIC EQUATIONS & INEQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - QUADRATIC EQUATIONS & INEQUATIONS EXERCISE - LEVEL -2
64 Videos
- QUADRATIC EQUATIONS & INEQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - QUADRATIC EQUATIONS & INEQUATIONS EXERCISE - Numerical value type of JEE Main
15 Videos
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - JEE Advanced (Archive)
50 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - MATHEMATICS
30 Videos
Similar Questions
Knowledge Check
The solution set of x−13+4<(x−55)−2 is
A(−∞,−50)B(−∞,−5)C(−∞,−10)D(−∞,−15)The solution set of |x−1|x>2 is
A0<x<13Bx<13Cx>13D13<x<1The solution set of −812<−12−4x<712,x∈W on the number line is:
A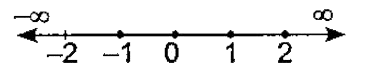 B
B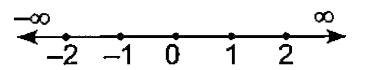 C
C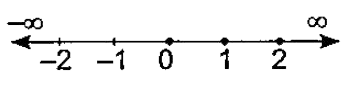 D
D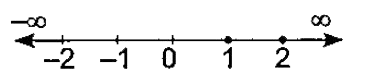
The solution set of (x+1x)2−32(x−1x) =4 when x≠0 is
View SolutionThe solution set of x2+x+|x|+1<0, is
View SolutionP is the solution set of 7x−2>4x+1andQ is the solution set of 9x−45≥5(x−5), where x∈R. Represent :
P∩Q
View SolutionP is the solution set of 7x−2>4x+1andQ is the solution set of 9x−45≥5(x−5), where x∈R. Represent :
P - Q
View SolutionSolution set of (5x−1)<(x+1)2<(7x−3) is
View Solution
