A bullet moving with a speed of 150ms−1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to shop after striking the tree?
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Initial velocity of the bullet, u=150m/s
- Final velocity of the bullet, v=0m/s (since it stops)
- Distance penetrated into the tree, x=3.5cm=3.5×10−2m
Step 2: Use the kinematic equation to find retardation (negative acceleration)
We can use the kinematic equation:
v2=u2+2ax
Rearranging the equation to solve for a:
0=(150)2+2a(3.5×10−2)
This simplifies to:
0=22500+0.07a
0.07a=−22500
a=−225000.07
Calculating the value:
a=−321428.57m/s2
The magnitude of the retardation is:
Retardation=321428.57m/s2
Step 3: Calculate the time taken to stop
We can use the formula for acceleration:
a=v−ut
Rearranging to find t:
t=v−ua
Substituting the values:
t=0−150−321428.57
This simplifies to:
t=−150−321428.57≈0.000466s
Converting to scientific notation:
t≈4.66×10−4s
Final Answers
- Magnitude of retardation: 321428.57m/s2
- Time taken to stop: 4.66×10−4s
---
- Initial velocity of the bullet, u=150m/s
- Final velocity of the bullet, v=0m/s (since it stops)
- Distance penetrated into the tree, x=3.5cm=3.5×10−2m
We can use the kinematic equation:
v2=u2+2ax
Rearranging the equation to solve for a:
0=(150)2+2a(3.5×10−2)
This simplifies to:
0=22500+0.07a
0.07a=−22500
a=−225000.07
Calculating the value:
a=−321428.57m/s2
The magnitude of the retardation is:
Retardation=321428.57m/s2
We can use the formula for acceleration:
a=v−ut
Rearranging to find t:
t=v−ua
Substituting the values:
t=0−150−321428.57
This simplifies to:
t=−150−321428.57≈0.000466s
Converting to scientific notation:
t≈4.66×10−4s
- Magnitude of retardation: 321428.57m/s2
- Time taken to stop: 4.66×10−4s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)
29 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A bullet moving at 20 m/sec. strikes a wooden plank and penetrates 4 cm before coming to stop. The time taken to stop is
View SolutionA bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
View SolutionA hammer of mass 1 kg moving with speed of 6ms−1 strikes a wall and comes to rest in 0.1 s . Calculate (i) the impules of force (ii) the retardation of the hammer , and (iii) the retarding that stops the hammer .
View SolutionA bullet initially moving with a velocity 20 m s−1 strikes a target and comes to rest after penetrating a distance 10 cm in the target. Calculate the retardation caused by the target.
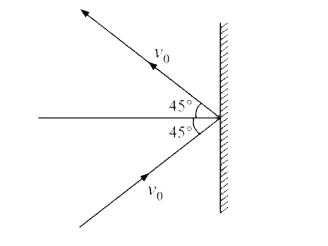
View SolutionA particle moving with speed v0=10√2ms−1 strikes a wall at an angle 45∘ as shown in figure. Find magnitude of change in velocity.
View SolutionA bullet of mass 5 g travelling with a speed of 210 m/s, strikes a fixed wooden target. One half of its kinetic energy is converted into heat in the bullet while the other half is converted into heat in the wood. The rise of temperature of the bullet if the specific heat of its material is 0.030 cal/(g−∘C)(1cal=4.2×107 ergs) close to :
View SolutionA bullet of mass 5 g travelling with a speed of 210 m/s, strikes a fixed wooden target. One half of its kinetic energy is converted into heat in the bullet while the other half is converted into heat in the wood. The rise of temperature of the bullet if the specific heat of its material is 0.030calg−∘C(1cal=4.2×107 ergs) close to :
View SolutionA bullet of mass 0.005 kg moving with a speed of 200 ms−1 enters a heavy wooden block and is stopped after a distance of 50 cm. What is the average force exerted by the block on the bullet?
View SolutionA bullet of mass 0.06 kg moving with a speed of 90ms−1 enters a heavy wooden block and it stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet ?
View SolutionA 2 kg block of wood rests on a long table top. A 5 g bullet moving horizontally with a speed of 150ms−1 is shot into the block and sticks to it. The block then slides 2.7m along the table top and comes to a stop. The force of friction between the block and the table is
View Solution
