An object describes 225 m in the first 3s and 400 m in the next 2s.Calculate the velocity after 5s.From the start.
To solve the problem, we need to calculate the velocity of the object after 5 seconds, given that it travels 225 m in the first 3 seconds and 400 m in the next 2 seconds. We will use the equations of motion to find the initial velocity and acceleration, and then use that information to find the final velocity.
1. Determine the distance traveled in each interval:
- Distance in the first 3 seconds (t1 = 3s): s1=225m
- Distance in the next 2 seconds (t2 = 2s): s2=400m
2. Calculate the total distance traveled in 5 seconds:
stotal=s1+s2=225m+400m=625m
3. Use the first segment of motion to find acceleration:
- We can use the equation of motion:
s=ut+12at2
For the first 3 seconds:
225=u(3)+12a(32)
Simplifying:
225=3u+92a(Equation 1)
4. Use the second segment of motion to find acceleration:
- For the next 2 seconds (from t = 3s to t = 5s):
400=u(2)+12a(22)
Simplifying:
400=2u+2a(Equation 2)
5. Now we have two equations (Equation 1 and Equation 2):
- From Equation 1:
3u+92a=225
- From Equation 2:
2u+2a=400
6. Rearranging Equation 2 to express u in terms of a:
2u=400−2a⟹u=200−a
7. Substituting u in Equation 1:
3(200−a)+92a=225
Expanding:
600−3a+92a=225
Combining terms:
600−225=3a−92a
375=6a−9a2⟹375=−3a2
Solving for a:
−3a=750⟹a=−250m/s2
8. Substituting a back to find u:
u=200−(−250)=450m/s
9. Now, calculate the final velocity after 5 seconds:
Using the formula:
v=u+at
Substituting u and a:
v=450+(−250)(5)=450−1250=−800m/s
Final Answer:
The velocity of the object after 5 seconds is −800m/s.
- Distance in the first 3 seconds (t1 = 3s): s1=225m
- Distance in the next 2 seconds (t2 = 2s): s2=400m
stotal=s1+s2=225m+400m=625m
- We can use the equation of motion:
s=ut+12at2
For the first 3 seconds:
225=u(3)+12a(32)
Simplifying:
225=3u+92a(Equation 1)
- For the next 2 seconds (from t = 3s to t = 5s):
400=u(2)+12a(22)
Simplifying:
400=2u+2a(Equation 2)
- From Equation 1:
3u+92a=225
- From Equation 2:
2u+2a=400
2u=400−2a⟹u=200−a
3(200−a)+92a=225
Expanding:
600−3a+92a=225
Combining terms:
600−225=3a−92a
375=6a−9a2⟹375=−3a2
Solving for a:
−3a=750⟹a=−250m/s2
u=200−(−250)=450m/s
Using the formula:
v=u+at
Substituting u and a:
v=450+(−250)(5)=450−1250=−800m/s
The velocity of the object after 5 seconds is −800m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Question for descriptiv Answers
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Short answer type question
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
An object covers 4m in the first two seconds and 4.4m in the next 4 seconds. Find its velocity after 7 seconds from the start.
View SolutionA body moving with uniform acceleration describes 40 m in the first 5 s and 70 m in the next 5 s.its initial velocity will be
View SolutionA body is moving with uniform acceleration covers 200 m in the first 2 s and 220 m in the next 4s. Find the velocity in ms−1 after 7 s.
View SolutionA body moving with uniform acceleration travels 84 m in the first 6 s and 180 m in the next 5 s. Find : (a) the initial velocity, and (b) the acceleration of the body.
View SolutionA force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate: The velocity acquired by the body
View SolutionAn object moves 10 m in 4 s then turns left and moves 20 m in next 5 s. What is the average speed of the object?
View SolutionIf acceleration of a particle at any time is given by a=2t+5
Calculate the velocity after 5 s, if it starts from rest
View SolutionStarting from a stationary position , Rahul paddles his bicycle to attain a velocity of 6m/s in 30s. Then he applies brakes such that the velocity of bicycle comes down to 4m/s in the next 5s . Calculate the acceleration of the bicycle in both the cases.
View SolutionThe average velocity of gas molecules is 400ms−1. Calculate their rms velocity at the same temperature.
View SolutionFig. 2.38 shows the displacement of a body at different times.
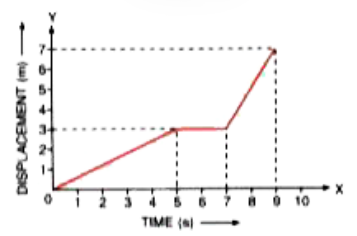
(a) Calculate the velocity of the body as it moves for time interval (i) 0 to 5 s,
(ii) 5 s to 7 S and
(iii) 7 s to 9 s.
(b) Calculate the average velocity during the time interval 5 s to 9 s. [Hint : From 5 s to 9 s, displacement = 7 m - 3 m = 4 m ]
View Solution
