An aeroplane requires a speed of 72 kmph for a take off with 150m run on the ground. The mass of the plane is 1500kg and the coefficient of friction between the aeroplane and the ground is 0.4. Assuming that the aeroplane acceleration uniformly during take off, find the minimum force exerted by the engine of the aeroplane for take off.
8500 N
7880 N
9000 N
6500 N
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Convert the speed from km/h to m/s
The speed required for takeoff is given as 72 km/h. We need to convert this to meters per second (m/s).
Speed in m/s=72 km/h×1000 m/km3600 s/h=20 m/s
Step 2: Use the kinematic equation to find acceleration
We know the initial speed u=0, final speed v=20 m/s, and the distance s=150 m. We can use the kinematic equation:
v2=u2+2as
Substituting the known values:
(20)2=0+2a(150)
400=300a
Solving for a:
a=400300=43 m/s2
Step 3: Calculate the frictional force
The frictional force ffriction can be calculated using the formula:
ffriction=μ⋅N
Where N is the normal force, which is equal to the weight of the airplane:
N=mg
Given:
- Mass m=1500 kg
- Coefficient of friction μ=0.4
- Acceleration due to gravity g=9.8 m/s2
Calculating N:
N=1500⋅9.8=14700 N
Now calculating the frictional force:
ffriction=0.4⋅14700=5880 N
Step 4: Calculate the minimum force exerted by the engine
Using Newton's second law, the net force F acting on the airplane is given by:
F=ma+ffriction
Substituting the values we have:
F=1500⋅43+5880
Calculating F:
F=2000+5880=7880 N
Conclusion
The minimum force exerted by the engine of the aeroplane for takeoff is:
7880 N
The speed required for takeoff is given as 72 km/h. We need to convert this to meters per second (m/s).
We know the initial speed u=0, final speed v=20 m/s, and the distance s=150 m. We can use the kinematic equation:
The frictional force ffriction can be calculated using the formula:
- Mass m=1500 kg
- Coefficient of friction μ=0.4
- Acceleration due to gravity g=9.8 m/s2
Using Newton's second law, the net force F acting on the airplane is given by:
The minimum force exerted by the engine of the aeroplane for takeoff is:
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
An aeroplane of mass 10,000 kg requires a speed of 20 ms−1 for take-off run of 100 m on the ground. The coefficient of kinetic friction between the wheels of the plane and ground is 0.3. Assume that the plane accelerates uniformly during the take off. Determine the minimum force required by the engine of the plane to take off (g=10ms−2).
View SolutionFind the force required to pull a block of mass 100kg up an incline of 8∘ at a uniform speed of 5m/s. The coefficient of friction between the block and the plane is 0.3.
View SolutionA car is taking a turn of radius 400 m on a horizontal circle . Coefficient of friction between the ground and tyres of car is 0.2 . Find the maximum speed with a safe turn can be taken
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA block A of mass 4kg is kept on ground. The coefficient of friction between the block and the ground is 0.8. The external force of magnitude 30N is applied parallel to the ground. The resultant force exerted by the ground on the block is (g=10m/s2) a) 40 N b) 30 N c) zero d) 50 N
View SolutionA block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k

View SolutionThe coefficient of friction between 4kg and 5kg blocks is 0.2 and between 5kg block, ground is 0.1 respectively. The minimum force 'F' required for slipping between 4kg and 5kg blocks is n×3 the value of n is.

View SolutionOn a stationary block of mass 2kg a horizontal forces F starts acting at t=0 whose veriation with time is shown in figure .The coefficient of friction between the block and ground is 0.5 New answer the following question
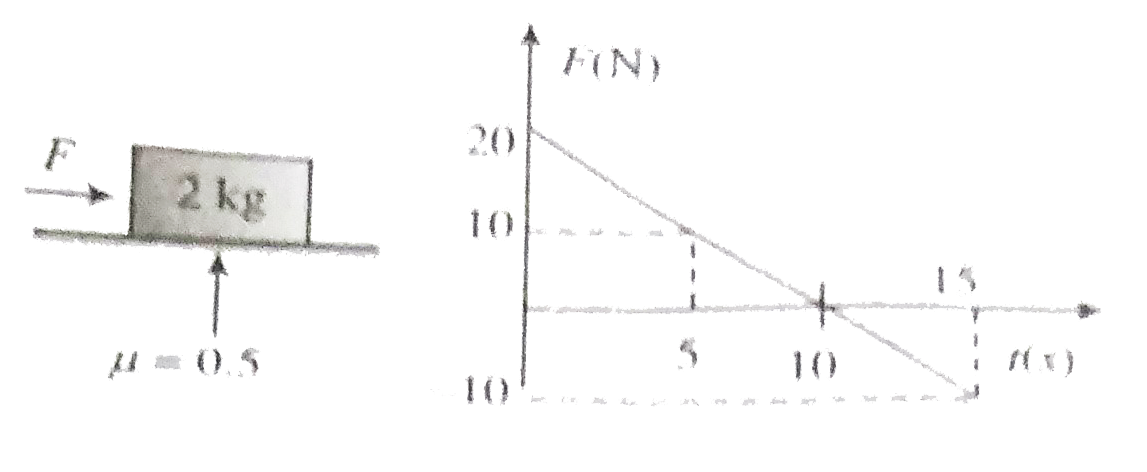
Find the time when acceleration of the block is zero
View SolutionA person of mass 75kg works in a where his job is to arrange heavy articles in a stone - room As shown in figure he place a packing of mass 20kg on a ramp that is inclined to the horizontal at 37∘ and pushed it up the ramp with an acceleration 1.5ms−2 .This is the minimum acceleration for the packege to reach the top to the ramp.THe coefficient of static and friction between the shoes of the person and the ground is 0.8 and coefficient of kinetic friction for the motion of package on the is 0.5
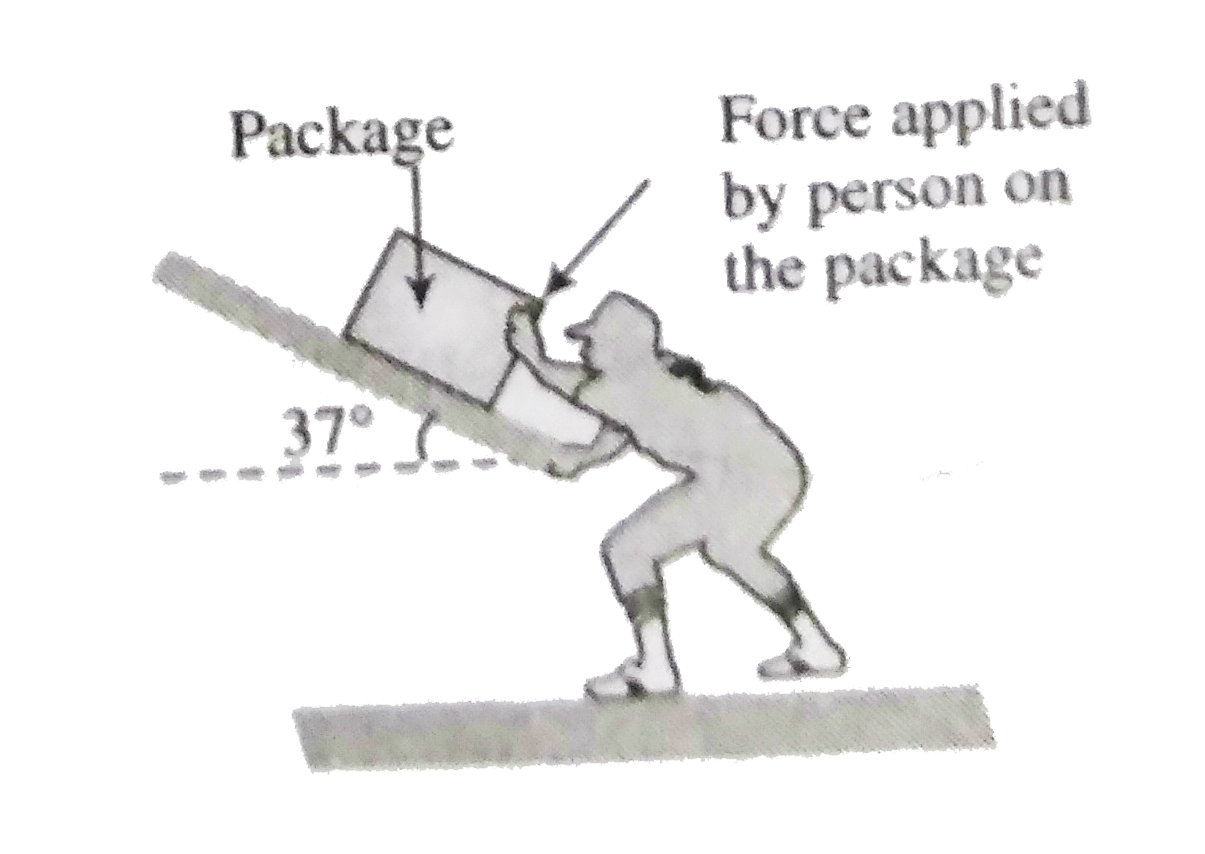
Force applied by the person on the package is
View SolutionA boy is pulshing a ring of mass 3 kg and radius 0.6 m with a stick as shown in figure. The stick applies a force of 3N on the ring and rolls it without slipping with an acceleration of 0.4 m/s2
 The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficeient of friction between the stick and the ring is f10 The vlaue of F is
The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficeient of friction between the stick and the ring is f10 The vlaue of F is
View Solution
