A block is placed on a ramp of parabolic shape given by the equation y=x2/20. If μs=0.5, then the maximum height above the ground at which the block can be placed without slipping is
Let the block can be placed on the ramp at a height h above the ground and θ is inclination of the ramp at the position. In the position the component of weight along the slope of ramp is mg sin θ downwards.

The limiting frictional force is =μsN=μsmgcosθ
In equilibrium, mgsinθ=msmgcosθqmgsinθ=tanθ=ms=0.5
but, y=x2/20
Slope tanθ=dydx=2x20=x10
x10=0.5⇒x=5
From the figure maximum height.
h=ymax=x220=2520=1.25m
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application6videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER5videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View SolutionA block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed on a surface with a vertical cross section given by y=x3/6. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is :
A1/2mB16mC2/3D1/3m
A disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View SolutionA parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .View Solution
.View SolutionA small block of mass 1kg is at rest on a parabolic surface given by y=x2. The coefficient of friction between the block and the surface is enough to prevent slipping.If position of block on surface is( 2m, 4m) then the normal force then the surface exerts at this position is
_PHY_E05_036_Q001.png) View Solution
View SolutionA small block of mass 1 kg is at rest on a parabolic surface given by y=x2. The coefficient of friction between the block and the surface is enough to prevent slipping. If position of block on surface is (2 m, 4 m), then the normal force that the surface exerts at this position is
_PHY_E05_190_Q04.png) View Solution
View SolutionThe coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.
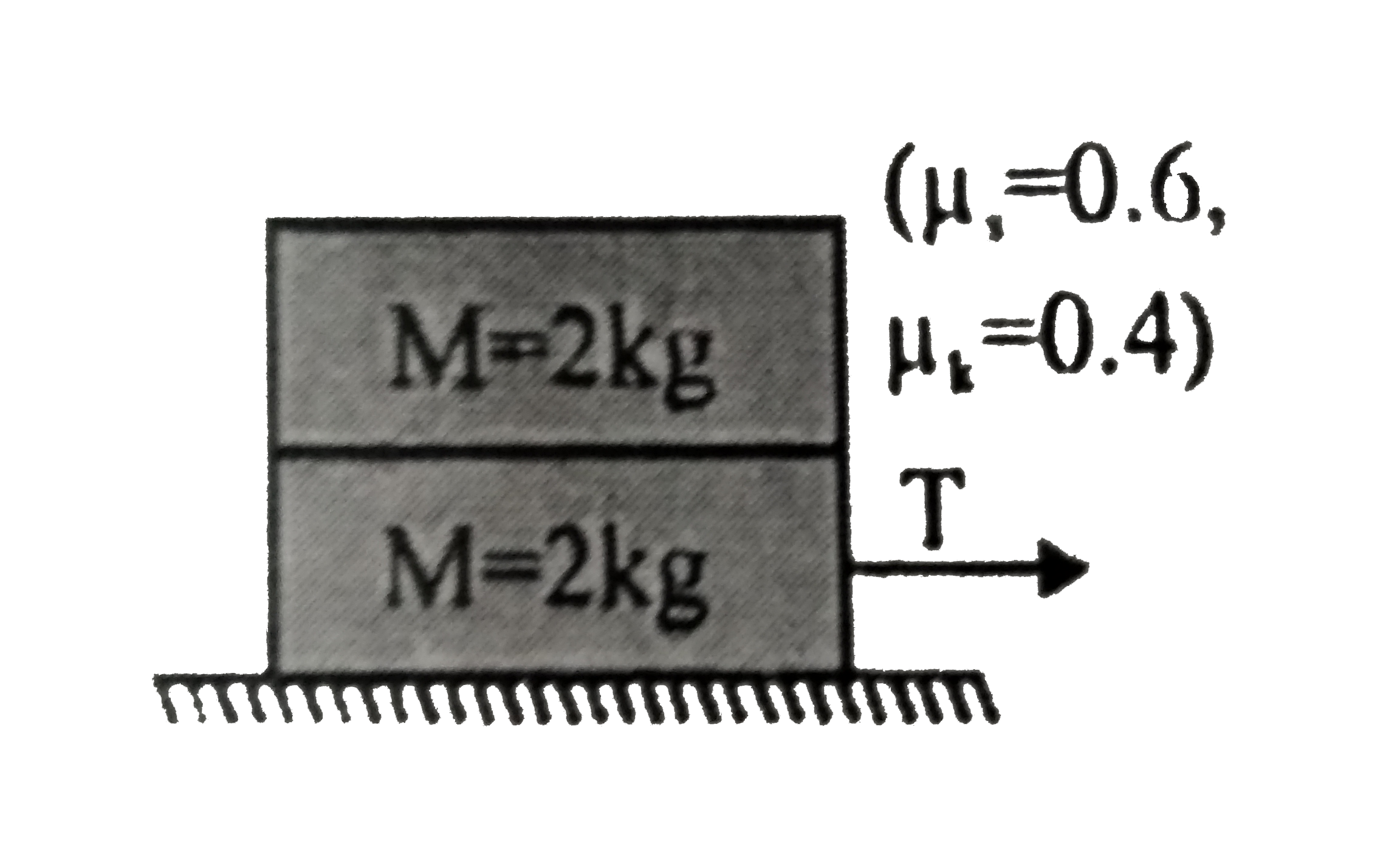 View Solution
View SolutionIn the diagram shown,the coefficient of friction between the blocks is equal to mu.Find out the maximum angular speed with which the system can be rotated so that no slipping takes place?
_PHY_E05_037_Q01.png) View Solution
View SolutionWith the assumption of no slipping, determine the mass m of the block which must be placed on the top of a 6kg cart in order that the system period is 0.75s. What is the minimum coefficient of static friction μs for which the block will not slip relative to the cart is displaced 50mm from the equilibrium position and released? Take (g=9.8m/s2).
 View Solution
View Solution

