A body moves along a circular path of radius 1m & μ=0.4. The maximum angular velocity in rad/sec of the body so that it does not slide is (g = 10ms−2)
2
30
15
4
The correct Answer is:A
To solve the problem, we need to find the maximum angular velocity of a body moving in a circular path without sliding, given the radius of the path, the coefficient of friction, and the acceleration due to gravity.
1. Identify the Given Values:
- Radius of the circular path, r=1m
- Coefficient of friction, μ=0.4
- Acceleration due to gravity, g=10m/s2
2. Understand the Forces Involved:
- For a body moving in a circular path, the centripetal force required to keep the body in circular motion is provided by the frictional force.
- The centripetal force Fc is given by:
Fc=mv2r
- The frictional force Ff is given by:
Ff=μmg
3. Set Up the Equation:
- For the body not to slide, the centripetal force must equal the frictional force:
mv2r=μmg
4. Cancel Out the Mass m:
- Since m appears on both sides of the equation, we can cancel it out:
v2r=μg
5. Substitute the Known Values:
- Substitute r=1m, μ=0.4, and g=10m/s2:
v21=0.4×10
v2=4
6. Find the Linear Velocity v:
- Taking the square root of both sides:
v=√4=2m/s
7. Relate Linear Velocity to Angular Velocity:
- The relationship between linear velocity v and angular velocity ω is given by:
v=rω
- Since r=1m:
2=1⋅ω
- Therefore, ω=2rad/s.
Final Answer:
The maximum angular velocity ω of the body so that it does not slide is:
ω=2rad/s
- Radius of the circular path, r=1m
- Coefficient of friction, μ=0.4
- Acceleration due to gravity, g=10m/s2
- For a body moving in a circular path, the centripetal force required to keep the body in circular motion is provided by the frictional force.
- The centripetal force Fc is given by:
Fc=mv2r
- The frictional force Ff is given by:
Ff=μmg
- For the body not to slide, the centripetal force must equal the frictional force:
mv2r=μmg
- Since m appears on both sides of the equation, we can cancel it out:
v2r=μg
- Substitute r=1m, μ=0.4, and g=10m/s2:
v21=0.4×10
v2=4
- Taking the square root of both sides:
v=√4=2m/s
- The relationship between linear velocity v and angular velocity ω is given by:
v=rω
- Since r=1m:
2=1⋅ω
- Therefore, ω=2rad/s.
The maximum angular velocity ω of the body so that it does not slide is:
ω=2rad/s
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II136videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
A rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)
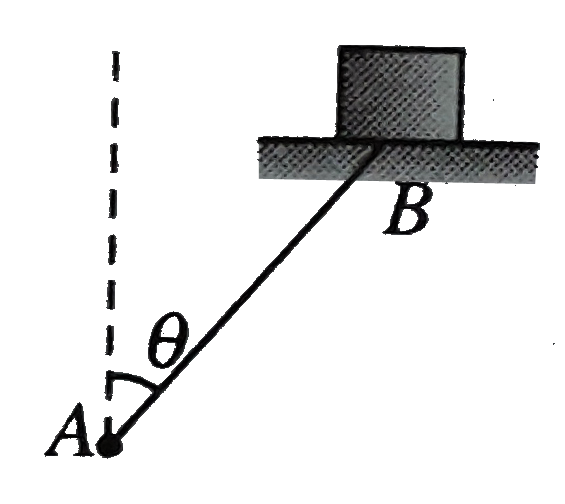 View Solution
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)
 View Solution
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA particle of mass 2 kg is moving along a circular path of radius 1 m. If its angular speed is 2π rad s−1, the centripetal force on it is
View SolutionA body moves along a circular path of radius 10m and the coefficient of friction is 0.5.What should be its angular speed (∈rads−1), if is not to slip from the surface ? (Given,g=9.8ms−2)
View SolutionIf 2 kg mass is rotating on a circular path of radius 0.8 m with angular velocity of 44 rad/sec. If radius of the parth becomes 1 m, then what will be the value of angular velocity?
View SolutionThe tangential acceleration of a particle moving in a circular path of radius 5cm is 2ms−2. The angular velocity of the particle increases from 10rads−1 to 20rads−1 during some time. Find
(a) this duration od time and
(b) the number of revolutions completed during this time.View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View SolutionDoes a body moving around a circular path with constant speed have constant velocity? Give reasons.
View Solution

