A block is placed at distance of 2m from the rear on the floor of a truck (g=10ms−2). When the truck moves with an acceleration of 8ms−2, the block takes 2 sec to fall off from the rear of the truck. The coefficient of sliding friction between truck and the block is
0.5
0.1
0.8
0.7
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of the block and the forces acting on it.
Step 1: Understand the scenario
- A block is placed on the floor of a truck that is accelerating forward with an acceleration A1=8m/s2.
- The block is initially at rest and is located 2 meters from the rear of the truck.
- The block takes 2 seconds to fall off the rear of the truck.
Step 2: Analyze the motion of the block
- The distance S that the block travels relative to the truck is 2 meters.
- The time T taken for the block to fall off is 2 seconds.
- The initial velocity U of the block is 0 (since it starts from rest).
Using the equation of motion:
S=Ut+12A2T2
where A2 is the acceleration of the block relative to the ground.
Substituting the known values:
2=0⋅2+12A2(22)
2=2A2
A2=1m/s2
Step 3: Set up the equation of motion for the block
- The block experiences a pseudo force due to the truck's acceleration, which is mA1 acting in the backward direction.
- The frictional force F acts in the forward direction.
Using Newton's second law, we have:
mA1−F=mA2
Substituting A1=8m/s2 and A2=1m/s2:
m⋅8−F=m⋅1
F=8m−1m=7m
Step 4: Relate frictional force to normal force
The frictional force F can also be expressed as:
F=μN
where N is the normal force. Since the block is on a horizontal surface, N=mg:
F=μmg
Step 5: Equate the two expressions for the frictional force
From the previous steps, we have:
μmg=7m
Dividing both sides by m (assuming m≠0):
μg=7
Substituting g=10m/s2:
μ⋅10=7
μ=710=0.7
Conclusion
The coefficient of sliding friction between the truck and the block is μ=0.7.
---
- A block is placed on the floor of a truck that is accelerating forward with an acceleration A1=8m/s2.
- The block is initially at rest and is located 2 meters from the rear of the truck.
- The block takes 2 seconds to fall off the rear of the truck.
- The distance S that the block travels relative to the truck is 2 meters.
- The time T taken for the block to fall off is 2 seconds.
- The initial velocity U of the block is 0 (since it starts from rest).
S=Ut+12A2T2
where A2 is the acceleration of the block relative to the ground.
2=0⋅2+12A2(22)
2=2A2
A2=1m/s2
- The block experiences a pseudo force due to the truck's acceleration, which is mA1 acting in the backward direction.
- The frictional force F acts in the forward direction.
mA1−F=mA2
Substituting A1=8m/s2 and A2=1m/s2:
m⋅8−F=m⋅1
F=8m−1m=7m
The frictional force F can also be expressed as:
F=μN
where N is the normal force. Since the block is on a horizontal surface, N=mg:
F=μmg
From the previous steps, we have:
μmg=7m
Dividing both sides by m (assuming m≠0):
μg=7
Substituting g=10m/s2:
μ⋅10=7
μ=710=0.7
The coefficient of sliding friction between the truck and the block is μ=0.7.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
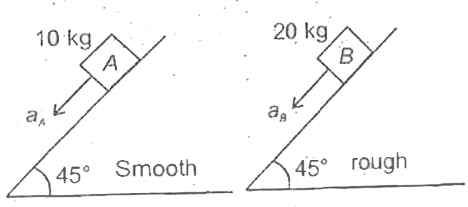
The ratio of acceleration of blocks A placed on smooth incline with block B placed on rough incline is 2:1. The coefficient of kinetic friction between block B and incline is
View SolutionA box is placed on the floor of a truck moving with an acceleration of 7ms−2. If the coefficient of kinetic friction between the box and surface of the truck is 0.5, find the acceleration of the box relative to the truck
View SolutionThe rear side of a truck is open and a box of mass 2kg is placed on the truck 8meters away from the open end. μ=0.1 and g=10m/s2. The truck starts from rest with an acceleration of 2m/s2 on a straight road. The box will fall off the truck when it is at distance from the starting point equal to
View SolutionThe rear side of a truck is open and a box of mass 20kg is placed on the truck 4m away from the open end μ=0.15 and g=10m/s2 The truck starts from rest with an acceleration of 2m/s2 on a straight road The box will fall off the truck when it is at a distance from the starting point equal to .
View SolutionDetermine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
View SolutionA lift is moving downwards with an acceleration equal to g. A block of mass m , kept on the floor of the lift of friction coefficient μ , is pulled horizontally . The friction acting on the block is
View SolutionA person drops a stone from a building of height 20 m. At the same instant the front end of a truck passes below the building moving with constant acceleration of 1m/s2 and velocity of 2m/s at that instant. Length of the truck if the stone just misses to hit its rear part is :-
View SolutionA block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA block of mass 10kg pushed by a horizontal force F on a horizontal rough plane moves with an aceleration 5ms−2. When force is doubled, its acceleration becomes 18ms−2. The coefficient of friction is (g=10ms−2)
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is (g=10ms−2)
View Solution
