The marks obtained by 10 students are as follows. Find their mean, median and mode. Also find M.D. from mean median and mode 15,10,6,15,12,9,3,5,4,2
The correct Answer is:mean = 8.1, median = 7.5 mode = 15, M.D. from mean = 41
M.D. from median = 4.1
M.D. from mode = 6.9
To solve the problem of finding the mean, median, mode, and mean deviation from the mean, median, and mode of the given marks obtained by 10 students, we will proceed step by step.
Step 1: Organize the Data
First, we need to arrange the marks in ascending order.
Given Marks:
15, 10, 6, 15, 12, 9, 3, 5, 4, 2
Sorted Marks:
2, 3, 4, 5, 6, 9, 10, 12, 15, 15
Step 2: Calculate the Mean
The mean is calculated using the formula:
Mean=Sum of observationsNumber of observations
Sum of Observations:
2+3+4+5+6+9+10+12+15+15=81
Number of Observations:
10
Mean Calculation:
Mean=8110=8.1
Step 3: Calculate the Median
To find the median, we need to identify the middle value(s). Since there are 10 observations (an even number), the median will be the average of the 5th and 6th values.
5th Value: 6
6th Value: 9
Median Calculation:
Median=6+92=152=7.5
Step 4: Calculate the Mode
The mode is the value that appears most frequently in the data set.
In our sorted data:
2, 3, 4, 5, 6, 9, 10, 12, 15, 15
The value 15 appears twice, while all other values appear only once.
Mode:
15
Step 5: Calculate Mean Deviation from Mean, Median, and Mode
Mean deviation is calculated using the formula:
Mean Deviation=∑|X−Measure|N
where X is each observation, "Measure" is the mean, median, or mode, and N is the number of observations.
Mean Deviation from Mean
1. Calculate |X−Mean|:
- For 2: |2 - 8.1| = 6.1
- For 3: |3 - 8.1| = 5.1
- For 4: |4 - 8.1| = 4.1
- For 5: |5 - 8.1| = 3.1
- For 6: |6 - 8.1| = 2.1
- For 9: |9 - 8.1| = 0.9
- For 10: |10 - 8.1| = 1.9
- For 12: |12 - 8.1| = 3.9
- For 15: |15 - 8.1| = 6.9 (twice)
Sum of Deviations from Mean:
6.1+5.1+4.1+3.1+2.1+0.9+1.9+3.9+6.9+6.9=41
Mean Deviation from Mean:
Mean Deviation from Mean=4110=4.1
Mean Deviation from Median
1. Calculate |X−Median|:
- For 2: |2 - 7.5| = 5.5
- For 3: |3 - 7.5| = 4.5
- For 4: |4 - 7.5| = 3.5
- For 5: |5 - 7.5| = 2.5
- For 6: |6 - 7.5| = 1.5
- For 9: |9 - 7.5| = 1.5
- For 10: |10 - 7.5| = 2.5
- For 12: |12 - 7.5| = 4.5
- For 15: |15 - 7.5| = 7.5 (twice)
Sum of Deviations from Median:
5.5+4.5+3.5+2.5+1.5+1.5+2.5+4.5+7.5+7.5=42
Mean Deviation from Median:
Mean Deviation from Median=4210=4.2
Mean Deviation from Mode
1. Calculate |X−Mode|:
- For 2: |2 - 15| = 13
- For 3: |3 - 15| = 12
- For 4: |4 - 15| = 11
- For 5: |5 - 15| = 10
- For 6: |6 - 15| = 9
- For 9: |9 - 15| = 6
- For 10: |10 - 15| = 5
- For 12: |12 - 15| = 3
- For 15: |15 - 15| = 0 (twice)
Sum of Deviations from Mode:
13+12+11+10+9+6+5+3+0+0=69
Mean Deviation from Mode:
Mean Deviation from Mode=6910=6.9
Final Results
- Mean: 8.1
- Median: 7.5
- Mode: 15
- Mean Deviation from Mean: 4.1
- Mean Deviation from Median: 4.2
- Mean Deviation from Mode: 6.9
First, we need to arrange the marks in ascending order.
15, 10, 6, 15, 12, 9, 3, 5, 4, 2
2, 3, 4, 5, 6, 9, 10, 12, 15, 15
The mean is calculated using the formula:
Mean=Sum of observationsNumber of observations
2+3+4+5+6+9+10+12+15+15=81
10
Mean=8110=8.1
To find the median, we need to identify the middle value(s). Since there are 10 observations (an even number), the median will be the average of the 5th and 6th values.
6th Value: 9
Median=6+92=152=7.5
The mode is the value that appears most frequently in the data set.
2, 3, 4, 5, 6, 9, 10, 12, 15, 15
15
Mean deviation is calculated using the formula:
Mean Deviation=∑|X−Measure|N
where X is each observation, "Measure" is the mean, median, or mode, and N is the number of observations.
1. Calculate |X−Mean|:
- For 2: |2 - 8.1| = 6.1
- For 3: |3 - 8.1| = 5.1
- For 4: |4 - 8.1| = 4.1
- For 5: |5 - 8.1| = 3.1
- For 6: |6 - 8.1| = 2.1
- For 9: |9 - 8.1| = 0.9
- For 10: |10 - 8.1| = 1.9
- For 12: |12 - 8.1| = 3.9
- For 15: |15 - 8.1| = 6.9 (twice)
6.1+5.1+4.1+3.1+2.1+0.9+1.9+3.9+6.9+6.9=41
Mean Deviation from Mean=4110=4.1
1. Calculate |X−Median|:
- For 2: |2 - 7.5| = 5.5
- For 3: |3 - 7.5| = 4.5
- For 4: |4 - 7.5| = 3.5
- For 5: |5 - 7.5| = 2.5
- For 6: |6 - 7.5| = 1.5
- For 9: |9 - 7.5| = 1.5
- For 10: |10 - 7.5| = 2.5
- For 12: |12 - 7.5| = 4.5
- For 15: |15 - 7.5| = 7.5 (twice)
5.5+4.5+3.5+2.5+1.5+1.5+2.5+4.5+7.5+7.5=42
Mean Deviation from Median=4210=4.2
1. Calculate |X−Mode|:
- For 2: |2 - 15| = 13
- For 3: |3 - 15| = 12
- For 4: |4 - 15| = 11
- For 5: |5 - 15| = 10
- For 6: |6 - 15| = 9
- For 9: |9 - 15| = 6
- For 10: |10 - 15| = 5
- For 12: |12 - 15| = 3
- For 15: |15 - 15| = 0 (twice)
13+12+11+10+9+6+5+3+0+0=69
Mean Deviation from Mode=6910=6.9
- Mean: 8.1
- Median: 7.5
- Mode: 15
- Mean Deviation from Mean: 4.1
- Mean Deviation from Median: 4.2
- Mean Deviation from Mode: 6.9
Similar Questions
Find the mean, median and mode of the following data

View SolutionFind the mean, median and mode of the following data :

View SolutionFind mean, median and mode of the following data :
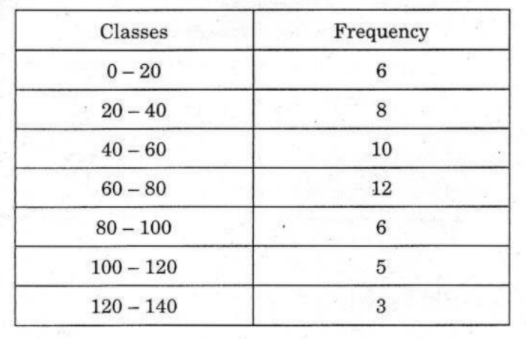
View SolutionFind out the mean & mode 1,3,1,6,4
View SolutionFind the mean, median and mode of the following data:
19, 7, 7, 25, 7
View SolutionThe runs scored in a cricket match by 11 players are as follows: Find the mean, mode and median of this data.
View SolutionThe scores in mathematics test (out of 25) of 15 students are as follows: Find the mode and median of this data. Are they same?
View SolutionFind mean, median and mode of the following data : 10, 12, 14, 16, 14
View SolutionThe following table gives the marks of 5 students in Science and Maths.

Find the mean, median, and mode of the marks scored in Science
View SolutionThe marks obtained by 30 students in a class assessment of 5 subjects is given below :

Calculate the mean, median and mode of the above distribution.
View Solution
