i. Mean = a (3 median - mode)
II. Mean - Mode = b(Mean - Median)
(iii) Median = Mode + c (Mean - mode)
The correct Answer is:A
To solve the problem, we need to establish the relationships between the constants a, b, and c based on the given equations involving mean, median, and mode.
1. Understanding the Standard Relation:
The standard relation between mean, median, and mode is given by:
3×Median=Mode+2×Mean
This will be our reference point for deriving the values of a, b, and c.
2. Finding a:
The first equation given is:
Mean=a×(3×Median−Mode)
From the standard relation, we can rearrange it to express Mean:
2×Mean=3×Median−Mode
Dividing both sides by 2 gives:
Mean=12×(3×Median−Mode)
Thus, we can conclude:
a=12
3. Finding b:
The second equation given is:
Mean−Mode=b×(Mean−Median)
Rearranging the standard relation, we have:
3×Median−Mean=Mode−Mean
Multiplying both sides by -1 gives:
Mean−Mode=3×(Mean−Median)
Therefore, we can conclude:
b=3
4. Finding c:
The third equation given is:
Median=Mode+c×(Mean−Mode)
From the standard relation, we can express Median as:
Median=13×Mode+23×Mean
Rearranging gives:
Median=Mode−23×Mode+23×Mean
This implies:
c=23
5. Establishing the Inequality:
Now we have:
a=12,b=3,c=23
We can compare these values:
12<23<3
Hence, we conclude:
a<c<b
Final Result:
The relationships between a, b, and c are:
a<c<b
The standard relation between mean, median, and mode is given by:
3×Median=Mode+2×Mean
This will be our reference point for deriving the values of a, b, and c.
The first equation given is:
Mean=a×(3×Median−Mode)
From the standard relation, we can rearrange it to express Mean:
2×Mean=3×Median−Mode
Dividing both sides by 2 gives:
Mean=12×(3×Median−Mode)
Thus, we can conclude:
a=12
The second equation given is:
Mean−Mode=b×(Mean−Median)
Rearranging the standard relation, we have:
3×Median−Mean=Mode−Mean
Multiplying both sides by -1 gives:
Mean−Mode=3×(Mean−Median)
Therefore, we can conclude:
b=3
The third equation given is:
Median=Mode+c×(Mean−Mode)
From the standard relation, we can express Median as:
Median=13×Mode+23×Mean
Rearranging gives:
Median=Mode−23×Mode+23×Mean
This implies:
c=23
Now we have:
a=12,b=3,c=23
We can compare these values:
12<23<3
Hence, we conclude:
a<c<b
The relationships between a, b, and c are:
a<c<b
Similar Questions
For a frequency distribution, mean, median and mode are connected by the relation (a) Mode = 3 Mean – 2 median (b) Mode = 2 Median – 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionOne of the methods of determining mode is (a) Mode = 2 Median – 3 Mean (b) Mode = 2 Median + 3 Mean (c) Mode = 3 Median – 2 Mean (d) Mode = 3 Median + 2 Mean
View SolutionThe relationship between mean, median and mode for a moderately skewed distribution is (a) Mode = 2 Median – 3 Mean (b) Mode = Median – 2 Mean (c) Mode = 2 Median – Mean (d) Mode = 3 Median – 2 mean
View SolutionFind the median and mode of the data:
View SolutionFind the mean deviation using median:
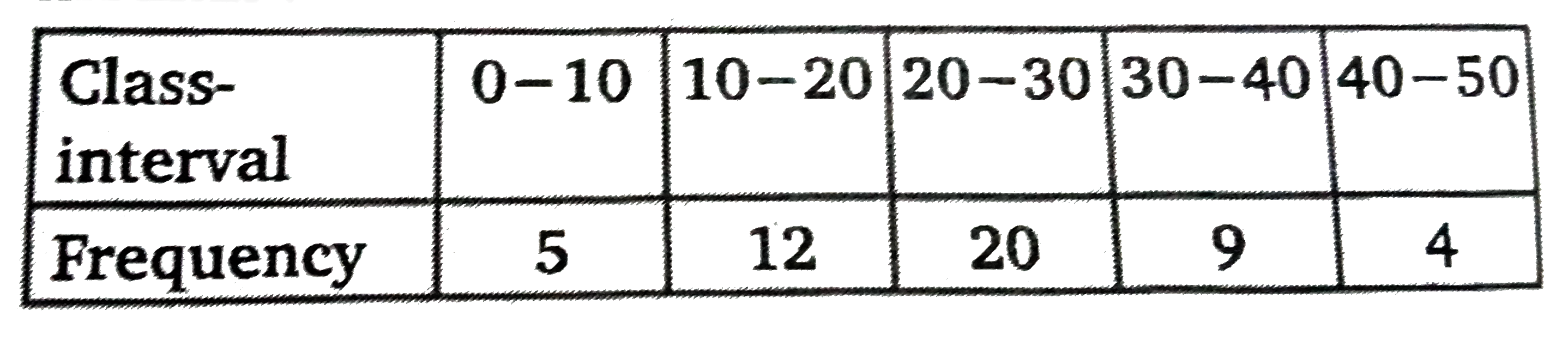
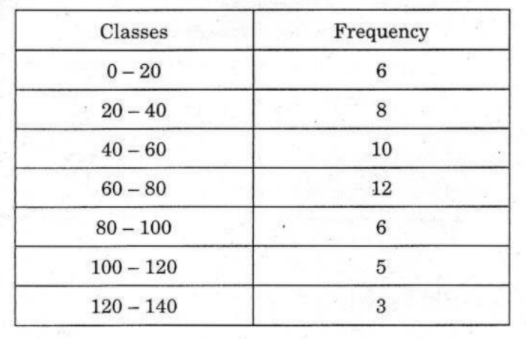
View SolutionFind mean, median and mode of the following data :
View SolutionFor a normal distribution if the mean is M, mode is M0 and median is Md, then
View SolutionWhich of the following is not a measure of central tendency? (a) Mean (b) Median (c) Mode (d) Standard deviation
View SolutionIf the difference of mode and median of a data is 24, then the difference of median and mean is (a) 12 (b) 24 (c) 8 (d) 36
View SolutionStatement-1 : If the mode of the data is 18 and the mean is 24, then median is 22
Statement-2 : Mode =3 median -2 mean A.Statement -1 is true , statement -2 is true B.Statement -1 is true but statement -2 is false. C.Statement -1 is false but statement -2 is true. D.none of these
View Solution
