The starting value of the model class of a distribution is 20. The frequency of the model class is 18. The frequencies of the classes preceeding and succeeding are 8,10 and the width of the model class is 5, then mode is
18.5
20.5
21.4
22.78
The correct Answer is:D
To find the mode of the given distribution, we will use the formula for the mode in a grouped frequency distribution. The formula is:
Mode=L+(F0−F−12F0−F−1−F1)×H
Where:
- L = lower boundary of the modal class
- F0 = frequency of the modal class
- F−1 = frequency of the class preceding the modal class
- F1 = frequency of the class succeeding the modal class
- H = width of the modal class
Step 1: Identify the given values
From the question, we have:
- L=20
- F0=18
- F−1=8
- F1=10
- H=5
Step 2: Substitute the values into the formula
Now, we will substitute these values into the mode formula:
Mode=20+(18−82×18−8−10)×5
Step 3: Simplify the expression
First, calculate the numerator and the denominator:
Numerator:
F0−F−1=18−8=10
Denominator:
2F0−F−1−F1=2×18−8−10=36−8−10=18
Now substitute these back into the formula:
Mode=20+(1018)×5
Step 4: Calculate the fraction
Now calculate the fraction:
1018=59
Step 5: Multiply by the width
Now multiply by H:
59×5=259
Step 6: Add to the lower boundary
Now add this to the lower boundary L:
Mode=20+259
To add these, convert 20 into a fraction with a denominator of 9:
20=1809
So:
Mode=1809+259=2059
Step 7: Calculate the final value
Now calculate 2059:
2059≈22.777…
Rounding this to two decimal places gives us:
Mode≈22.78
Final Answer
Thus, the mode of the distribution is approximately 22.78.
- L = lower boundary of the modal class
- F0 = frequency of the modal class
- F−1 = frequency of the class preceding the modal class
- F1 = frequency of the class succeeding the modal class
- H = width of the modal class
From the question, we have:
- L=20
- F0=18
- F−1=8
- F1=10
- H=5
Now, we will substitute these values into the mode formula:
First, calculate the numerator and the denominator:
F0−F−1=18−8=10
2F0−F−1−F1=2×18−8−10=36−8−10=18
Now calculate the fraction:
Now multiply by H:
Now add this to the lower boundary L:
Now calculate 2059:
Thus, the mode of the distribution is approximately 22.78.
Similar Questions
The mean of the following distribution is 18. Find the frequency f of the class 19−21.
View SolutionConsider the data

The frequency of the upper limit of the median class and the lower limit of the modal class is
View SolutionThe mean of the following distribution is 52 and the frequency of class interval 30-40 is f. Find f.
View SolutionConsider the following distribution
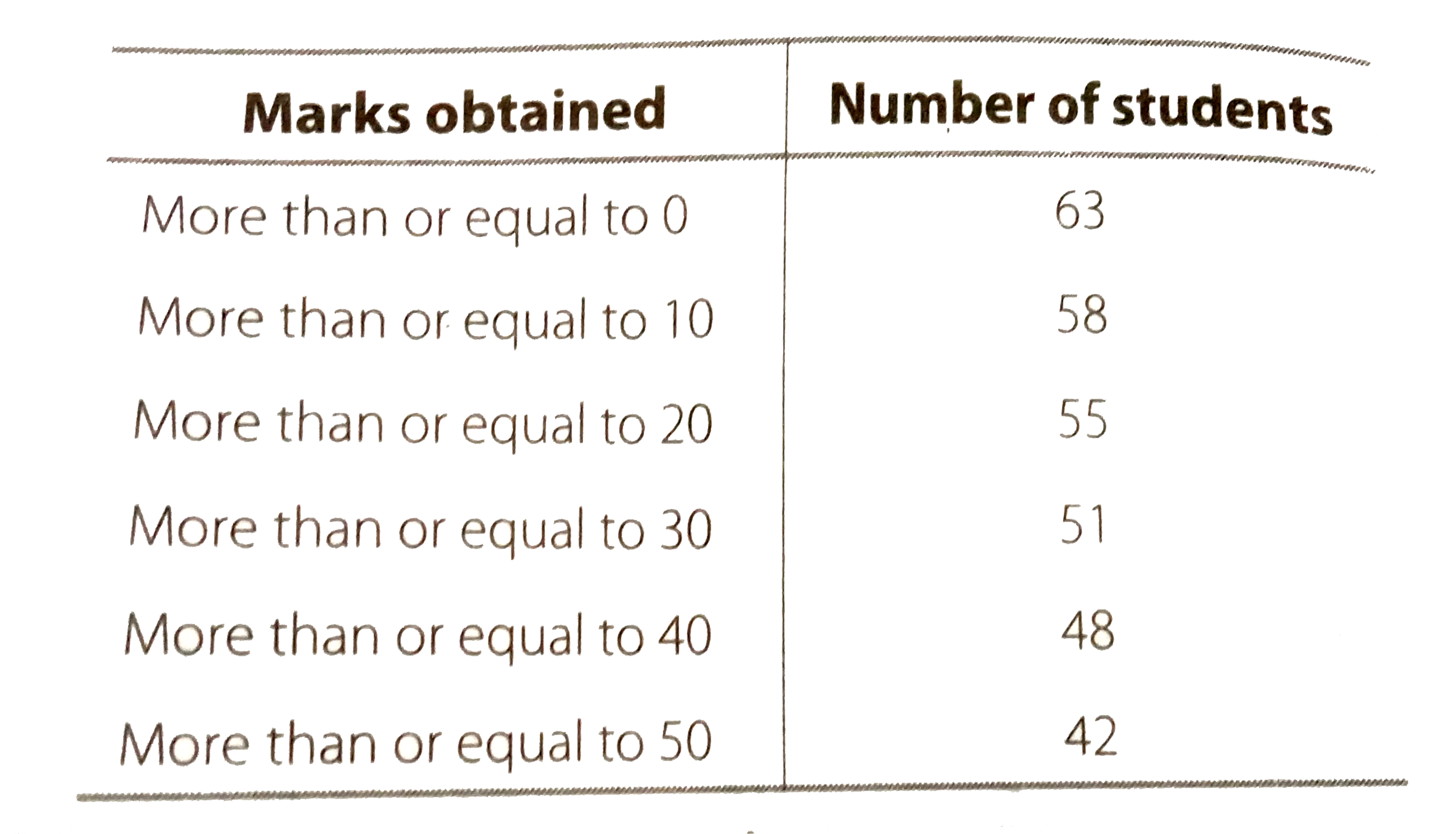
Frequency of the class 30-40 is
View SolutionWhile calculating mode the following observation are found. Lower limit of modal class =40, frequency of modal class =20, frequency of previous class =12 , frequency of preceding class =11 and width of the class =10, find mode .
View SolutionThe class marks of a distribution are 12, 18, 24, 30. Find the class interval.
View SolutionConsider the following frequency distribution

The upper limit of the median class in
View SolutionIn a frequency distribution, the mid values of a class is 10 and width of the class is 6. The lower limit of the class is
View SolutionFor the following frequency distribution

The upper limit of median class is
View SolutionWrite the comulative frequency of class interval 30-40

View Solution
