The point of intersection of the asymptotes with the directrices lie on
The correct Answer is:a2
Step by step video & image solution for The point of intersection of the asymptotes with the directrices lie on by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The line 2x+y=3 intersects the ellipse 4x2+y2=5 at two points. The point of intersection of the tangents to the ellipse at these point is
View SolutionFind the point of intersection of the tangents drawn to the curve x2y=1−y at the points where it is intersected by the curve xy=1−y.
View SolutionGiven ellipse x216+y217=1 and the hyperbola x2144−y281=125 , if the ordinate of one of the points of intersection is produced to cut asymptote at P, then which of the following is true?
View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side
View SolutionThe number of points of intersection of diagonals which lie within the decagon: ^10C2 b. ^10C4 c. ^10C6+1 d. 10+10C2
View SolutionShow that the tangent at any point of a hyperbola cuts off a triangle of constant area from the asymptotes and that the portion of it intercepted between the asymptotes is bisected at the point of contact.
View SolutionThe points of intersection of the parabolas y2=5x and x2=5y lie on the line
View SolutionIn a hyperbola, the portion of the tangent intercepted between the asymptotes is bisected at the point of contact.
Consider a hyperbola whose center is at the origin. A line x+y=2 touches this hyperbola at P(1,1) and intersects the asymptotes at A and B such that AB = 6√2 units.
The equation of the pair of asymptotes is
View SolutionIn a hyperbola, the portion of the tangent intercepted between the asymptotes is bisected at the point of contact.
Consider a hyperbola whose center is at the origin. A line x+y=2 touches this hyperbola at P(1,1) and intersects the asymptotes at A and B such that AB = 6√2 units.
The equation of the tangent to the hyperbola at (−1,7/2) is
View SolutionForm Fig., write
(i)all pairs of parallel lines. (ii)all pairs of intersection lines. (iii)lines whose point of intersection is l . (iv) lines whose point of intersection is D . (v) lines whose point of intersection is E . (vi) lines whose point of intersection is A .
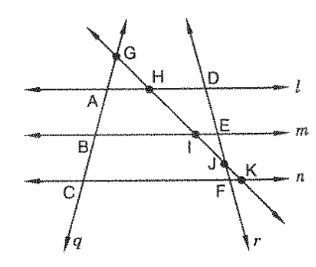
View Solution
