Ancient mammals enjoyed a release from competition when the dinosaurs became extinct. Should humans work to ensure that such releases from competition continue to occur for us or for other species?
No, because it is impossible to predict which pecies will become dominant if other species become extinct will cause the extinction of humans.
No, because the species that become dominant will cause the extinction of humans.
Yes, because the organisms that are released from competition will always form more new species then the number that went extinct
Yes, because new species that evolve are always better organisms than those that went extinct
The correct Answer is:A
Step-by-Step Solution
1. Understanding the Context: The question refers to the historical event when dinosaurs became extinct, allowing ancient mammals to thrive without competition. This sets the stage for discussing whether humans should seek similar situations of reduced competition for themselves or other species.
2. Analyzing the Implications of Extinction: When a species goes extinct, it can create opportunities for other species to dominate. However, predicting which species will thrive in the absence of another is complex and uncertain.
3. Evaluating the Consequences: If humans were to facilitate the extinction of certain species to reduce competition, it could lead to unforeseen consequences. The newly dominant species might not be beneficial for the ecosystem or for humans themselves.
4. Considering Ecological Balance: Ecosystems are interconnected. The extinction of one species can have a ripple effect, potentially leading to the decline of other species, including humans. Thus, promoting extinction for competition relief could be harmful.
5. Conclusion: Based on the analysis, it is concluded that humans should not work to ensure releases from competition through the extinction of other species. This is primarily because it is impossible to predict the outcomes of such actions, and they could lead to negative consequences for both humans and other species.
Final Answer
Humans should not work to ensure that releases from competition continue to occur for us or for other species, as it could lead to unpredictable and potentially harmful consequences for the ecosystem.
---
Humans should not work to ensure that releases from competition continue to occur for us or for other species, as it could lead to unpredictable and potentially harmful consequences for the ecosystem.
Topper's Solved these Questions
- EVOLUTIONBOOK - AAKASH SERIESCHAPTER - EVOLUTIONEXERCISE - EXERCISE - I (EVOLUTION OF MAN)
27 Videos
- EVOLUTIONBOOK - AAKASH SERIESCHAPTER - EVOLUTIONEXERCISE - EXERCISE -II (ORIGIN OF LIFE AND EVOLUTION OF LIFE FORMS)
18 Videos
- EVOLUTIONBOOK - AAKASH SERIESCHAPTER - EVOLUTIONEXERCISE - EXERCISE - I (EVOLUTIONARY FORCES)
6 Videos
- DIGESTION AND ABSORPTIONBOOK - AAKASH SERIESCHAPTER - DIGESTION AND ABSORPTIONEXERCISE - Exercise - III (Previous AIPMT/NEET Questions)
24 Videos
- EXCRETORY PRODUCTS AND THEIR ELIMINATIONBOOK - AAKASH SERIESCHAPTER - EXCRETORY PRODUCTS AND THEIR ELIMINATIONEXERCISE - EXERCISE - III (PREVIOUS AIPMT/NEET QUESTIONS)
20 Videos
Similar Questions
When released from ovary, human egg contains
View SolutionIf an object is released in air, the magnitude of its acceleration would begain at the free-fall value, but it would decrease continously to zero as the object continued to fall.
for which one of the choices given does the solid line best represent the speed of the object as a function of time when it is dropped from rest in air?
Note The deshed line shows the free-fall under vacuum graph for comparison.
A.
B.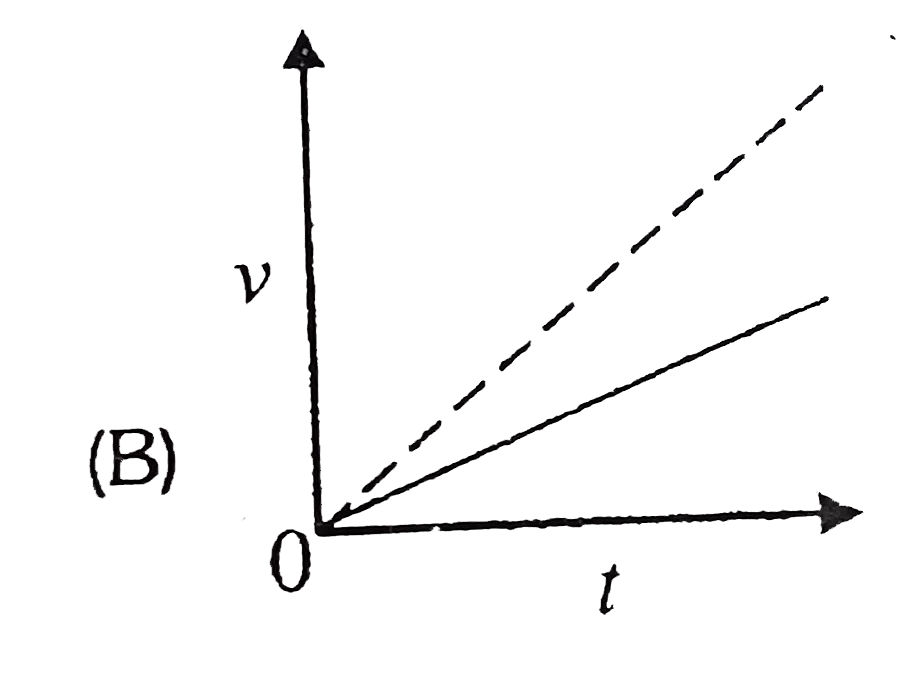
C.
D.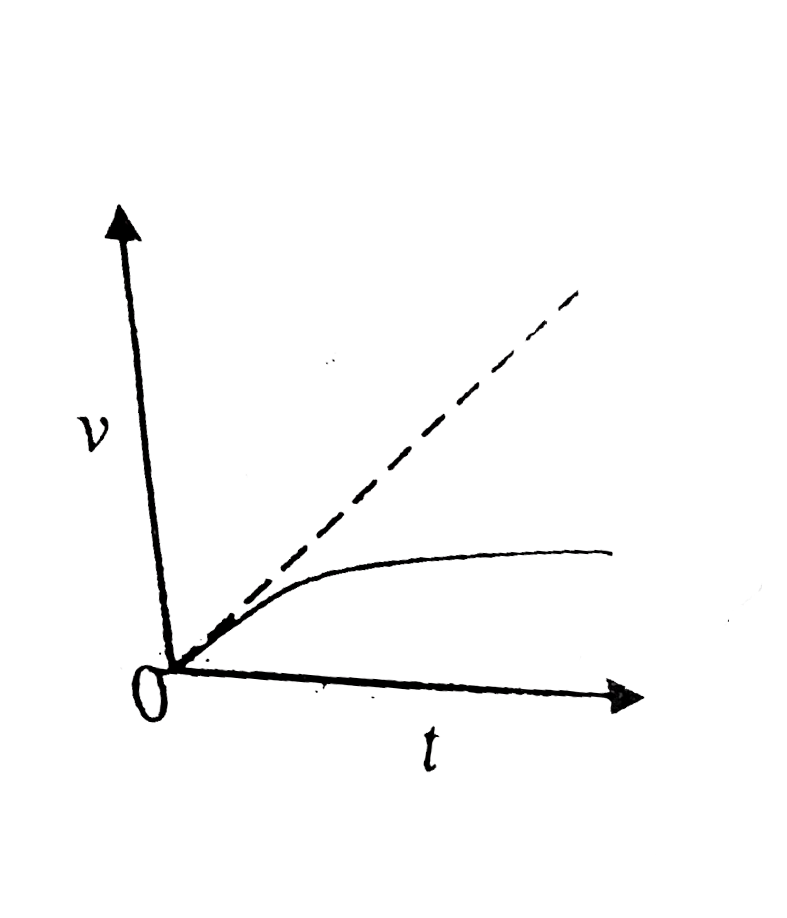
View Solution
Knowledge Check
Island biogeography theory states that the number of species on an island is determined by immigration rates of new species to the island and extinction rates of species on the island. Immigration rates to an island decline as its distance from the mainland increases adn extinction rates decreases with increasing island size. when the immigration and extinction rates on an island are equal, the number of species on the island reaches equilibrium.
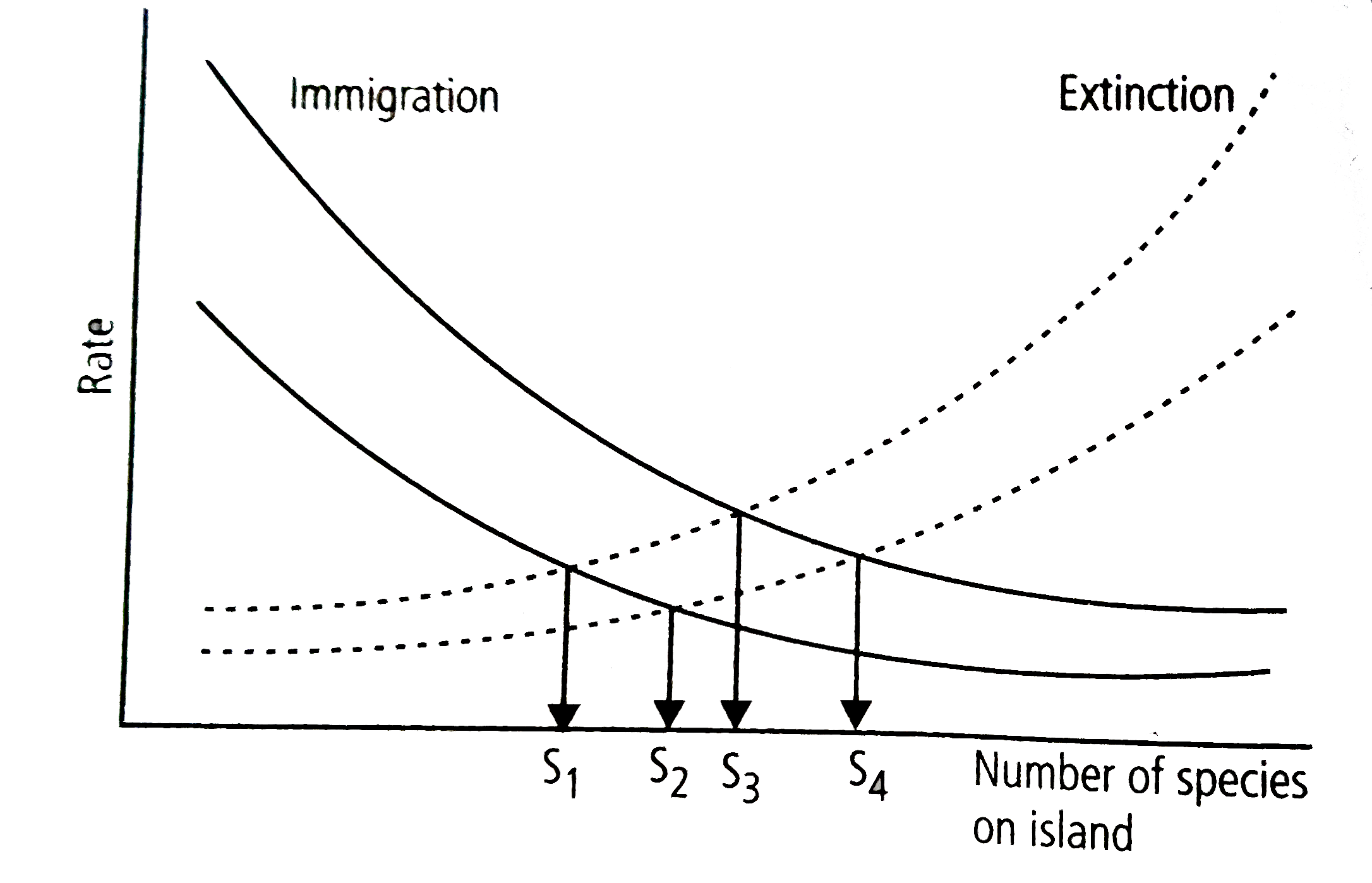
Which of the following gives the correct combination of distance (near and far) and area (small and large of islands where species (S1−S4) occur ?AS1− near island, small islandBS2− near island, large islandCS3− small island, far islandDS4 near island, large island
One end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View SolutionAssertion :- Due to continental drift pouched mammals of Australia survived.
Reason :- There is lack of competition from any other mammal.
View SolutionMore than 10 species of invertebrates became extinct within a year from the American pacific coast when Pisaster starfish was removed. This extinction was due to -
View SolutionIn the figure, block A is released from rest when the spring is its natural length for the block B of mass m to leave contact with the ground at some stage what should be the minimum mass of block A?
 .
.
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

View SolutionA ball of mass 1kg is suspended by an inextensible string 1m long attached to a point O of a smooth horizontal bar resting on fixed smooth supports A and B. The ball is released from rest from the position when the string makes an angle 30∘ with the vertical. The mass of the bar is 4kg. The displacement of bar when ball reaches the other extreme position (in m) is

View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
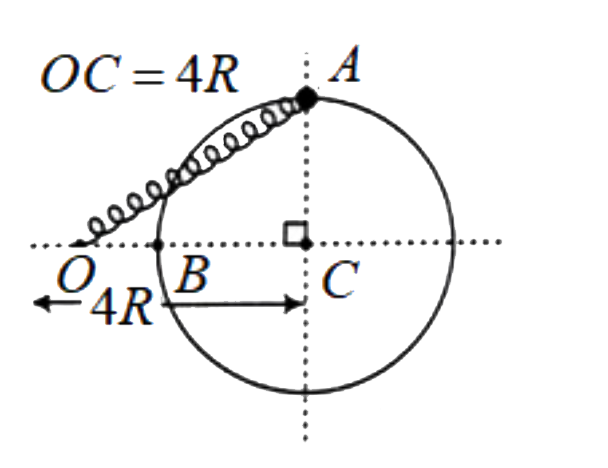
View Solution
