A student forgot Newton's formula for speed of sound but he knows there were speed (υ) pressure (p) and density (d) in the formula. He then starts using dimensional analysis method to find the actual relation. υ=kpxdy. Where k is a dimensionless constant on the basis of above passage answer the following questions.
The value of x is
1
12
−12
2
The correct Answer is:B
To find the value of x in the equation υ=kpxdy using dimensional analysis, we will follow these steps:
Step 1: Identify the dimensions of each variable
1. Speed (υ): The dimension of speed is LT−1 (length per time).
2. Pressure (p): Pressure is defined as force per unit area. The dimension of force is MLT−2, and area is L2. Therefore, the dimension of pressure is:
(p)=(F)(A)=MLT−2L2=ML−1T−2
3. Density (d): Density is defined as mass per unit volume. The dimension of volume is L3. Therefore, the dimension of density is:
(d)=(M)(V)=ML3=ML−3
Step 2: Write the dimensional equation
We can express the dimensions of υ in terms of p and d:
(LT−1)=(px)(dy)
Substituting the dimensions we found:
LT−1=(ML−1T−2)x(ML−3)y
Step 3: Expand the right-hand side
Expanding the right-hand side gives:
LT−1=Mx+yL−x−3yT−2x
Step 4: Equate the dimensions
Now we equate the dimensions on both sides:
1. For mass (M):
0=x+y(since there is no mass on the left side)
2. For length (L):
1=−x−3y
3. For time (T):
−1=−2x
Step 5: Solve the equations
From the time equation:
−1=−2x⟹x=12
Now substituting x=12 into the mass equation:
0=12+y⟹y=−12
Conclusion
The value of x is:
12
1. Speed (υ): The dimension of speed is LT−1 (length per time).
2. Pressure (p): Pressure is defined as force per unit area. The dimension of force is MLT−2, and area is L2. Therefore, the dimension of pressure is:
(p)=(F)(A)=MLT−2L2=ML−1T−2
3. Density (d): Density is defined as mass per unit volume. The dimension of volume is L3. Therefore, the dimension of density is:
(d)=(M)(V)=ML3=ML−3
We can express the dimensions of υ in terms of p and d:
(LT−1)=(px)(dy)
Substituting the dimensions we found:
LT−1=(ML−1T−2)x(ML−3)y
Expanding the right-hand side gives:
LT−1=Mx+yL−x−3yT−2x
Now we equate the dimensions on both sides:
1. For mass (M):
0=x+y(since there is no mass on the left side)
2. For length (L):
1=−x−3y
3. For time (T):
−1=−2x
From the time equation:
−1=−2x⟹x=12
0=12+y⟹y=−12
The value of x is:
12
Similar Questions
A student forgot Newton's formula for speed of sound but he knows there were speed (υ) pressure (p) and density (d) in the formula. He then starts using dimensional analysis method to find the actual relation. υ=kpxdy. Where k is a dimensionless constant on the basis of above passage answer the following questions.
If the density will increase the speed of sound will :
View SolutionIn a problem of differentiation of f(x)g(x), one student writes the derivative of f(x)g(x) as f'(x)g'(x) and he finds the correct result . If g(x)=x2andlimx→∞f(x)=4 On the basis of above information , answer the following questions :
The function f(x) is
View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the terminal speed of the object ?
View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the pattern of acceleration change of the body ?
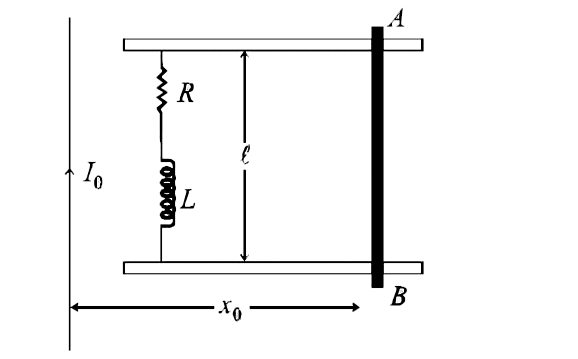
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
View SolutionA man of mass 50kg is runing on a plank of mass 150kg with speed of 8m/s relative to plank as shows in the figure (both were initially at rest and velocity of man with respect to ground any how remains constant). Plank is placed on smooth horizontal surface. The man, while runing, whistle with frequency fo. A detected (D) placed on plank detects frequency. The man jumps off with same velocity (w.r.t. to groung) from point D and slides on the smooth horizontal surface [Assume coefficient of friction between man and horizontal is zero]. The speed of sound in still medium is 330m/s. Answer the following questions on the basis of above situations.

The frequency of sound detected by D, after man jumps off the plank is
View SolutionA man of mass 50kg is runing on a plank of mass 150kg with speed of 8m/s relative to plank as shows in the figure (both were initially at rest and velocity of man with respect to ground any how remains constant). Plank is placed on smooth horizontal surface. The man, while running, whistle with frequency fo. A detected (D) placed on plank detects frequency. The man jumps off with same velocity (w.r.t. to ground) from point D and slides on the smooth horizontal surface [Assume coefficient of friction between man and horizontal is zero]. The speed of sound in still medium is 330m/s. Answer the following questions on the basis of above situations.

The frequency of sound detected by detector D, before man jumps of the plank is
View SolutionA man of mass 50kg is runing on a plank of mass 150kg with speed of 8m/s relative to plank as shows in the figure (both were initially at rest and velocity of man with respect to ground any how remains constant). Plank is placed on smooth horizontal surface. The man, while runing, whistle with frequency fo. A detected (D) placed on plank detects frequency. The man jumps off with same velocity (w.r.t. to groung) from point D and slides on the smooth horizontal surface [Assume coefficient of friction between man and horizontal is zero]. The speed of sound in still medium is 330m/s. Answer the following questions on the basis of above situations.

The frequency of sound detected by detector D, before man jumps of the plank is
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19C
Q. The speed of the particle that can take discrete values is proportional to
View Solution‘Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of anything between 100 metres – 300 metres.The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be raised properly and effectively.
Based on the following figure related to sky sailing, answer the questions
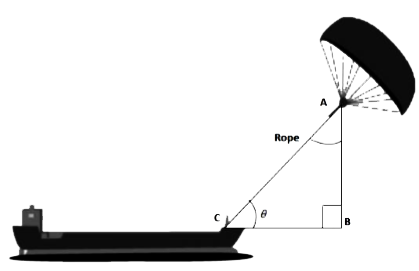
(i) In the given figure, if sinθ=cos(3θ−30∘), where θ and 3θ−30∘ are acuts angle, then find the value of θ.
(ii) What should be the length of the rope of the kite sail in order to pull the ship at the angle θ (calculated above) and be at a vertical height of 200 m?
View Solution
