A body of mass 'm' at rest is applied with a force F = (2 + 4t)N. The change in momentum of the interval one second to two second is
3kg−ms−1
4kg−ms−1
6kgms−1
8kgms−1
The correct Answer is:D
To solve the problem, we need to find the change in momentum of a body of mass 'm' when a force F=(2+4t)N is applied over the time interval from 1 second to 2 seconds. Here’s a step-by-step solution:
Step 1: Understanding the relationship between force and momentum
The change in momentum (ΔP) of an object is given by the integral of force over time:
ΔP=∫Fdt
Step 2: Substitute the given force into the equation
Given the force F=2+4t, we can substitute this into the momentum change equation:
ΔP=∫(2+4t)dt
Step 3: Set the limits of integration
We need to find the change in momentum from t=1s to t=2s. Therefore, we will integrate from 1 to 2:
ΔP=∫21(2+4t)dt
Step 4: Calculate the integral
Now we calculate the integral:
ΔP=(2t+2t2)21
This is because the integral of 4t is 2t2 and the integral of 2 is 2t.
Step 5: Evaluate the integral at the limits
Now we evaluate the expression at the upper and lower limits:
ΔP=(2(2)+2(22))−(2(1)+2(12))
Calculating this gives:
ΔP=(4+8)−(2+2)
ΔP=12−4=8kg m/s
Conclusion
Thus, the change in momentum of the body from 1 second to 2 seconds is:
ΔP=8kg m/s
The change in momentum (ΔP) of an object is given by the integral of force over time:
ΔP=∫Fdt
Given the force F=2+4t, we can substitute this into the momentum change equation:
ΔP=∫(2+4t)dt
We need to find the change in momentum from t=1s to t=2s. Therefore, we will integrate from 1 to 2:
ΔP=∫21(2+4t)dt
Now we calculate the integral:
ΔP=(2t+2t2)21
This is because the integral of 4t is 2t2 and the integral of 2 is 2t.
Now we evaluate the expression at the upper and lower limits:
ΔP=(2(2)+2(22))−(2(1)+2(12))
Calculating this gives:
ΔP=(4+8)−(2+2)
ΔP=12−4=8kg m/s
Thus, the change in momentum of the body from 1 second to 2 seconds is:
ΔP=8kg m/s
Similar Questions
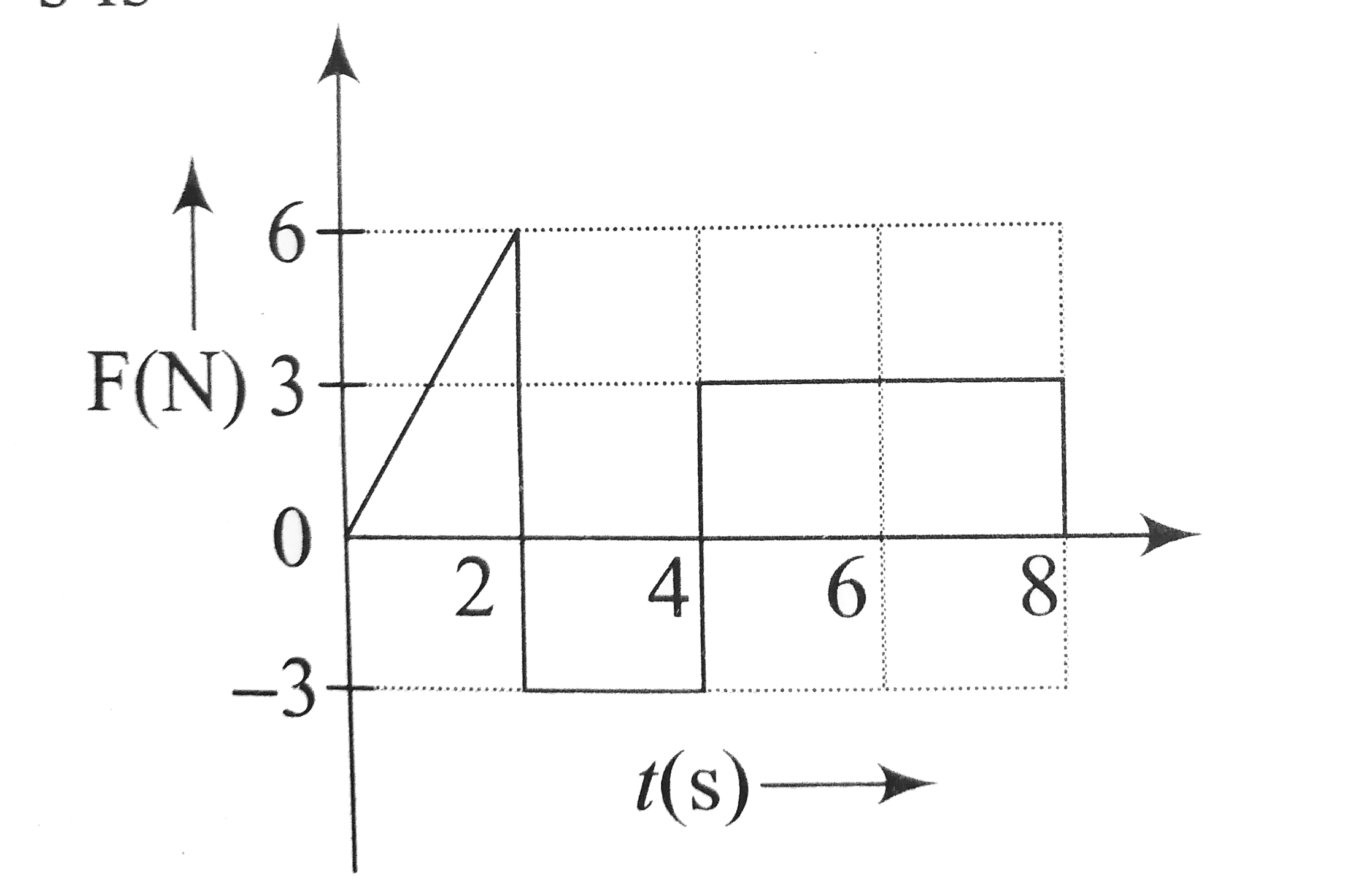
The force F acting on a partical of mass m is indicated by the force-time graph shown below. The change in momentum of the particle over time interval from zero to 8 s is.
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA body of mass 5kg initially at rest, is subjected to a force of 40 N. Find the kinetic energy acquired by the body at the end of 5 seconds :
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate change in momentum of the body.
View SolutionA body of mass 2 kg makes an elastic collision with a second body at rest and continues to move in the original direction but with one fourth of its original speed. What is the mass of the second body?
View SolutionThe force(F) acting on a particle of mass m changing with time(t) is as shown in (F−t) graph. The change in linear momentum from t=0 to t=6 s (in kN s) is

View SolutionThe force acting on a particle of mass 20 kg is indicated by force - time graph as shown in figure. The magnitude of change in linear momentum of particle during time interval 0 to 6 second is

View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and t = 1 s.
View SolutionA body is acted on by a force given by F = (10+2t) N. The impulse received by the body during the first four seconds is
View SolutionA time varying force F=6t−2t2N, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at t=0 the force F=0. Now answer the following:
Find the duration for which the force acts on the body.
View Solution
