If a pushing force making an angle α with horizontal is applied on a block of mass m placed on horizontal table and angle of friction is β, then minimum magnitude of force required to move the block is
mgsinβcos[α−β]
mgsinβcos[α+β]
mgsinβsin[α+β]
mgcosβcos[α−β]
To solve the problem of finding the minimum magnitude of the force required to move a block of mass m placed on a horizontal table when a pushing force F is applied at an angle α with the horizontal, we can follow these steps:
1. Identify Forces Acting on the Block:
- The weight of the block W=mg acts downward.
- The normal force N acts upward.
- The applied force F can be resolved into two components:
- Horizontal component: Fcosα
- Vertical component: Fsinα
2. Set Up the Vertical Force Balance:
- The vertical forces acting on the block can be expressed as:
N+Fsinα=mg
- Rearranging gives:
N=mg−Fsinα
3. Determine the Frictional Force:
- The frictional force f that opposes the motion is given by:
f=μN
- The coefficient of friction μ can be expressed in terms of the angle of friction β:
μ=tanβ
- Thus, the frictional force becomes:
f=tanβ⋅N=tanβ(mg−Fsinα)
4. Set Up the Horizontal Force Balance:
- For the block to just start moving, the horizontal component of the applied force must equal the frictional force:
Fcosα=f
- Substituting the expression for f:
Fcosα=tanβ(mg−Fsinα)
5. Rearranging the Equation:
- Expanding the right side:
Fcosα=sinβcosβ(mg−Fsinα)
- Rearranging gives:
Fcosα+Fsinαtanβ=mgtanβ
6. Factoring Out F:
- Factor F from the left side:
F(cosα+sinαtanβ)=mgtanβ
- This can be rewritten as:
F=mgtanβcosα+sinαtanβ
7. Simplifying the Expression:
- Substitute tanβ=sinβcosβ:
F=mgsinβcosβcosα+sinαsinβcosβ
- This simplifies to:
F=mgsinβcosαcosβ+sinαsinβ
- Using the angle addition formula, this can be expressed as:
F=mgsinβcos(α+β)
Final Result:
Thus, the minimum magnitude of the force required to move the block is:
F=mgsinβcos(α+β)
- The weight of the block W=mg acts downward.
- The normal force N acts upward.
- The applied force F can be resolved into two components:
- Horizontal component: Fcosα
- Vertical component: Fsinα
- The vertical forces acting on the block can be expressed as:
N+Fsinα=mg
- Rearranging gives:
N=mg−Fsinα
- The frictional force f that opposes the motion is given by:
f=μN
- The coefficient of friction μ can be expressed in terms of the angle of friction β:
μ=tanβ
- Thus, the frictional force becomes:
f=tanβ⋅N=tanβ(mg−Fsinα)
- For the block to just start moving, the horizontal component of the applied force must equal the frictional force:
Fcosα=f
- Substituting the expression for f:
Fcosα=tanβ(mg−Fsinα)
- Expanding the right side:
Fcosα=sinβcosβ(mg−Fsinα)
- Rearranging gives:
Fcosα+Fsinαtanβ=mgtanβ
- Factor F from the left side:
F(cosα+sinαtanβ)=mgtanβ
- This can be rewritten as:
F=mgtanβcosα+sinαtanβ
- Substitute tanβ=sinβcosβ:
F=mgsinβcosβcosα+sinαsinβcosβ
- This simplifies to:
F=mgsinβcosαcosβ+sinαsinβ
- Using the angle addition formula, this can be expressed as:
F=mgsinβcos(α+β)
Thus, the minimum magnitude of the force required to move the block is:
F=mgsinβcos(α+β)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA body of mass 10 kg is placed on rough surface, pulled by force F making an angle of 30∘ above the horizontal. If the angle of friction is also 30∘, then the minimum magnitude of force F required to move the body is equal to ( take, g=10ms−2)
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
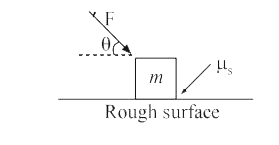
View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block

View SolutionMinimum horizontal force (F) required to move the block shown in diagram is__
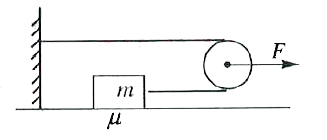
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View Solution
