A merry go round has a radius 4 m and completes a revolution in 2 seconds. Then acceleration of a point on its rim is
4π2
2π2
π2
Zero
The correct Answer is:A
To find the acceleration of a point on the rim of a merry-go-round, we can follow these steps:
1. Identify the given parameters:
- Radius of the merry-go-round, r=4m
- Time period for one complete revolution, T=2s
2. Calculate the linear velocity v:
The formula for linear velocity in circular motion is given by:
v=2πrT
Substituting the values:
v=2π×42=4πm/s
3. Calculate the centripetal acceleration ac:
The formula for centripetal acceleration is:
ac=v2r
First, calculate v2:
v2=(4π)2=16π2
Now substitute v2 and r into the centripetal acceleration formula:
ac=16π24=4π2m/s2
4. Final Result:
The acceleration of a point on the rim of the merry-go-round is:
ac=4π2m/s2
- Radius of the merry-go-round, r=4m
- Time period for one complete revolution, T=2s
The formula for linear velocity in circular motion is given by:
v=2πrT
Substituting the values:
v=2π×42=4πm/s
The formula for centripetal acceleration is:
ac=v2r
First, calculate v2:
v2=(4π)2=16π2
Now substitute v2 and r into the centripetal acceleration formula:
ac=16π24=4π2m/s2
The acceleration of a point on the rim of the merry-go-round is:
ac=4π2m/s2
Similar Questions
A partical revolves in clockwise direction (as seen from point A) in a circle C of radius 1 cm and completes one revolution in 2 sec. The axis of the circle and the principal axis of the mirror M coincides, call it AB. The radius of curvature of the mirror of 20cm. Then, the direction of revolution (as seen from A) of the image of the partical and its speed is
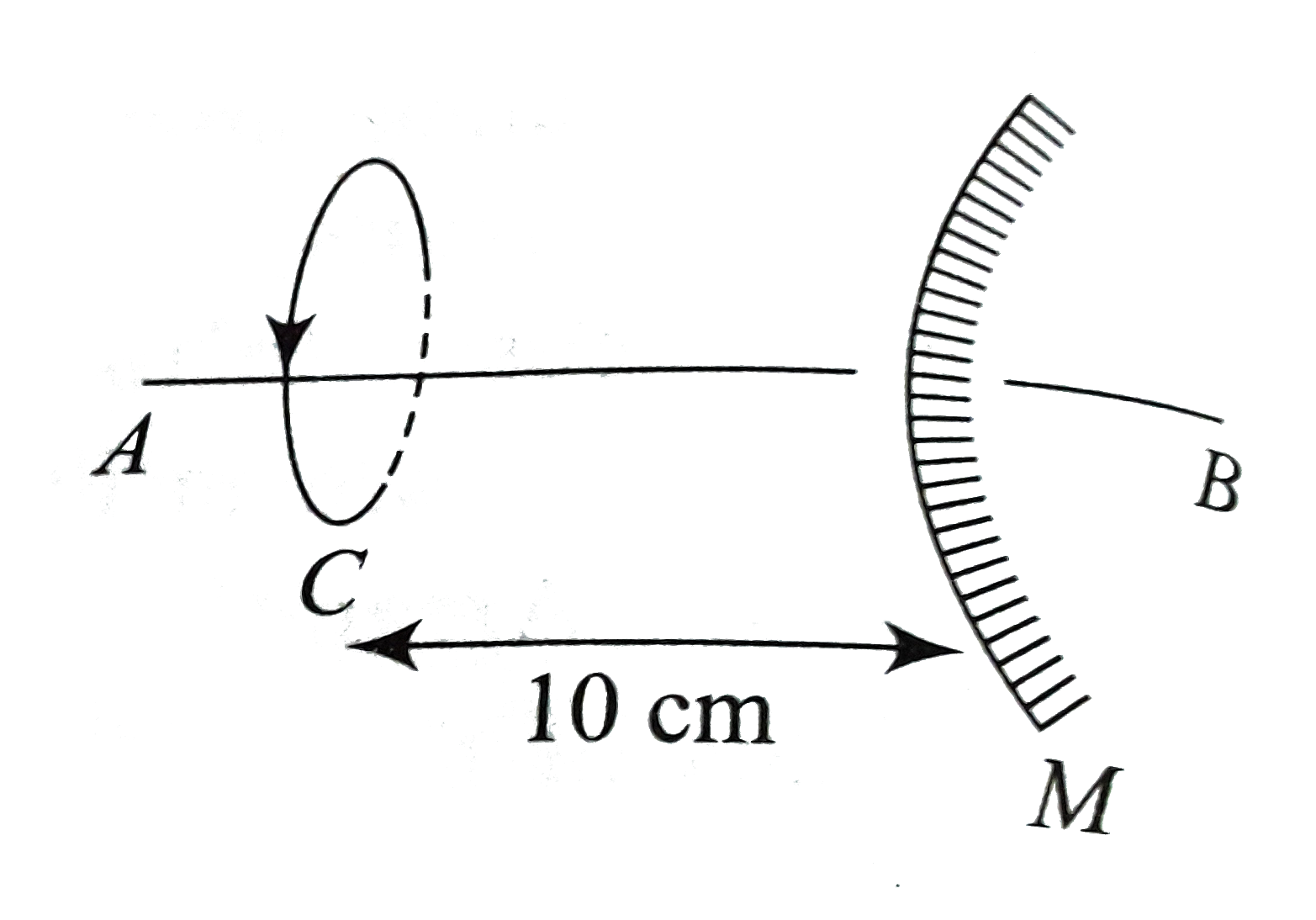
View SolutionA particle moves in a circle of radius 25 cm at 2 revolution per second. The acceleration of the particle in meter per second2 is
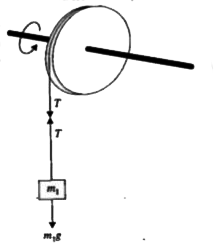
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
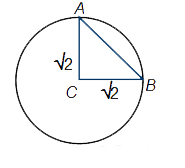
View SolutionA man starts running with constant speed along a circular path of radius √2m He completes two rounds in 16 seconds. The magnitude of the average velocity in first 2 seconds is
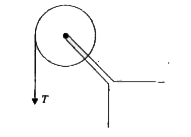
View SolutionFig. shows a uniform disc of mass 1 kg and radius 0.2 m mounted on an axle supported in fixed frictionless bearings. A light string is wrapped around the rim of the wheel. A constant downwards pull of 2 kg wt. is exerted on the string. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ?
View SolutionThe radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. find the acceleration due to the gravitation of the plane at its surface.
View SolutionA satellite moving in a circular orbit at an altitude of 1000 km completes one revolution round the earth in 105 minutes. What is (z) its angular velocity and speed? Radius of the earth =6.4×106m.
View SolutionA body performing uniform cicular motion completed 140 revolution in a second. Its angular speed is
View SolutionA particle is moving along a circle such that it completes one revolution in 40 seconds. In 2 minuts 20 seconds, the ratio |displacement|distance is distance
View SolutionDrops of water are thrown tangentially of the horizontal rim of a rotating wet umbrella. The rim is 3ft in diameter and is held 4ft above the ground and makes 14 revolutions in 33 seconds. Drops of water will meet the ground on a circle of diameter (in ft).
View Solution
