A wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
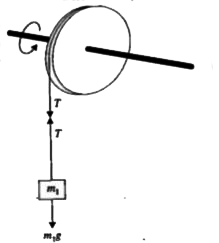
Mass of wheel = m = 1.4 kg
Radius = r=0.4 m
Angular acceleration of the wheel =α= ?
τ=Iα=Tr
12mrα=T
tangential acceleration a=rα
T=12ma
When the mass falls downwards with an acceleration a,
m1g−T=m1a
m1g−12ma=m1a
a(m1+m2)=m1g,a=m1gm1+m2=2×9.82+1.42
Tangential accelerations =a=7.26m/s2
Angular acceleration =α=ar=7.260.4=18.15m/s2
Tension in the string =T=12ma=12×1.4×7.26=5.1N
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
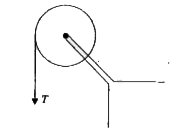
Fig. shows a uniform disc of mass 1 kg and radius 0.2 m mounted on an axle supported in fixed frictionless bearings. A light string is wrapped around the rim of the wheel. A constant downwards pull of 2 kg wt. is exerted on the string. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ?
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.
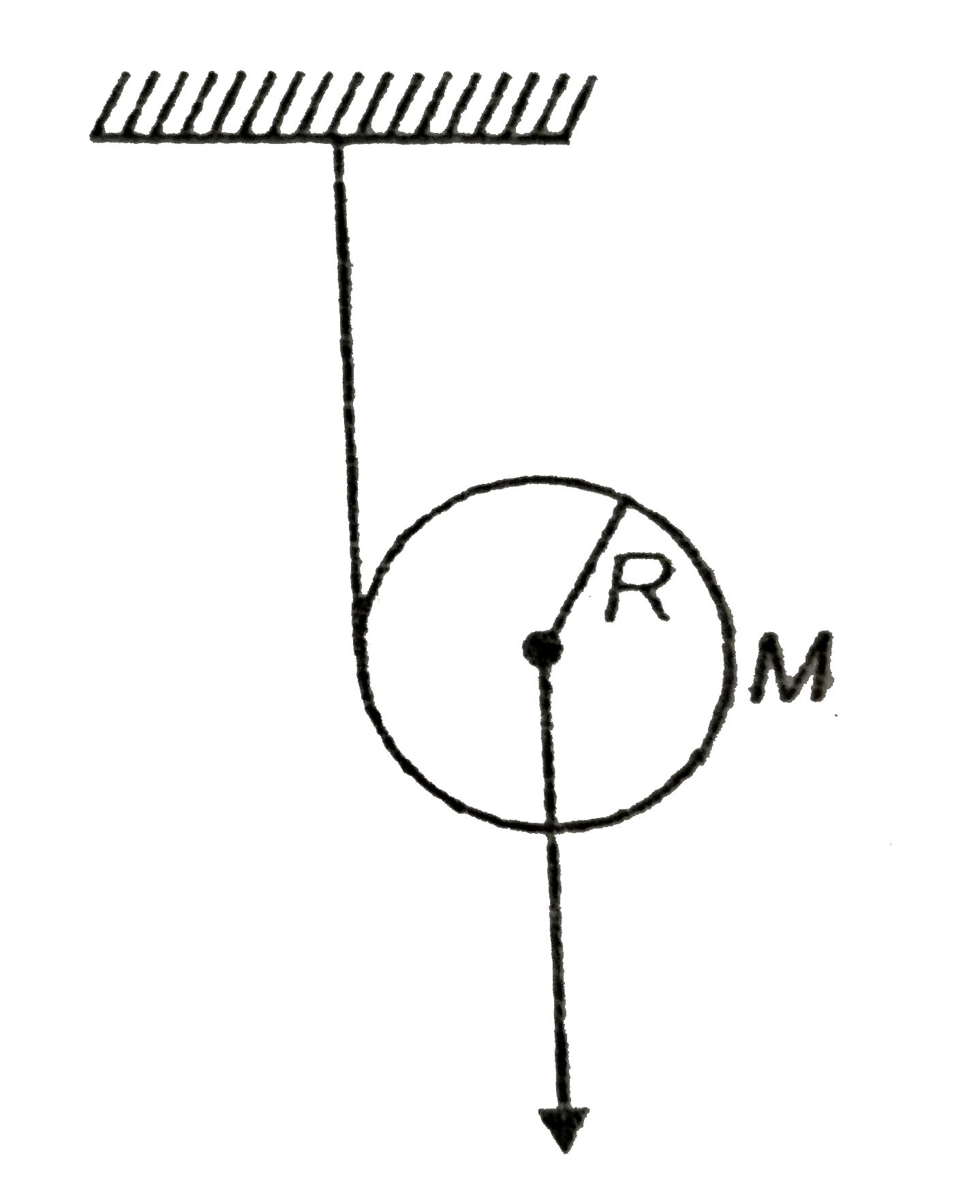
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
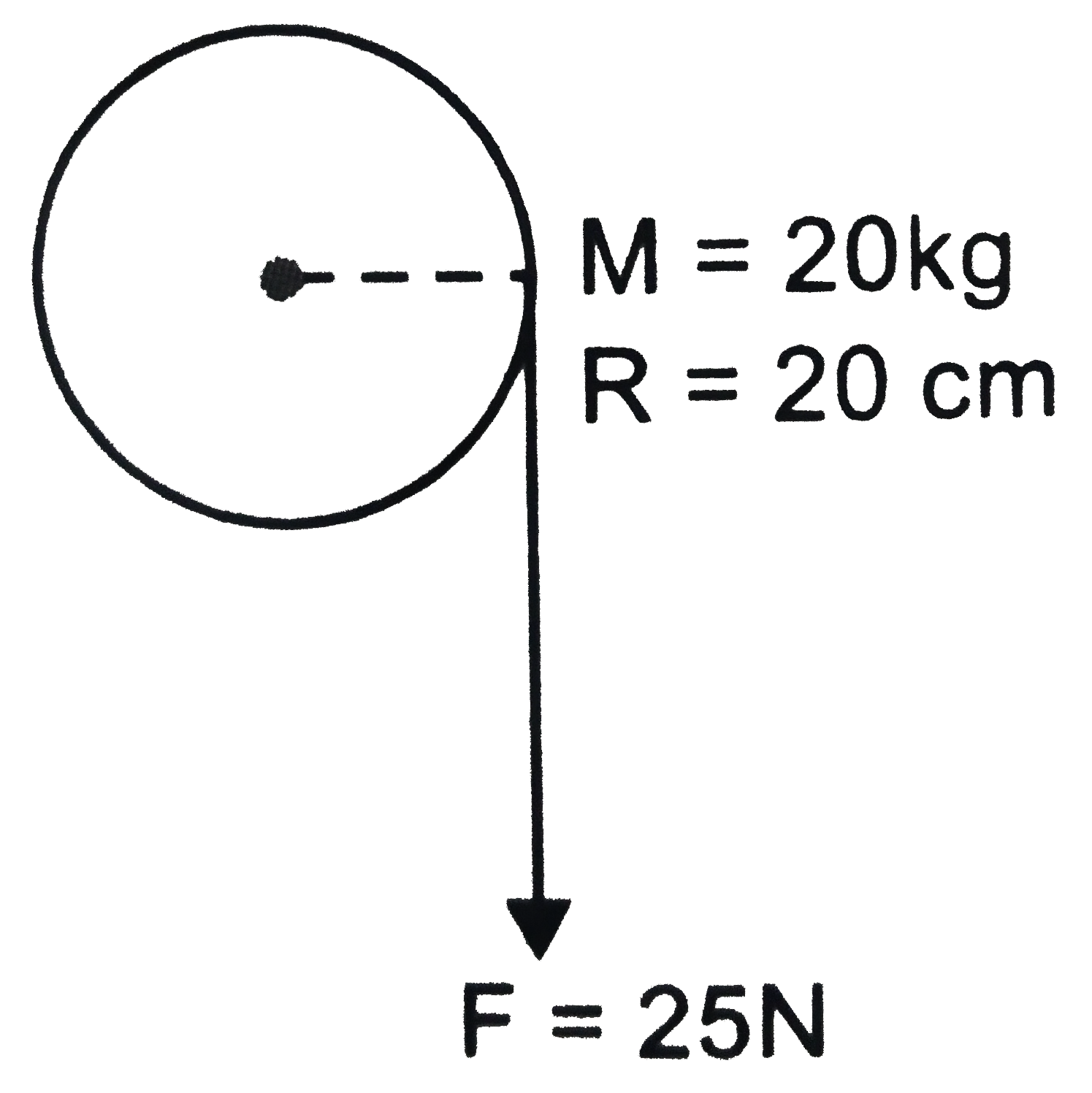
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionA string is wound around a hollow cylinder of mass 5 Kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string).
View Solution