A body of mass m is made to revolve along a circle of radius r in horizontal plane at a speed Vm/s with help of light horizontal string such that the tension in the string is 10 N. Keeping speed constant if mass is increased to 2m und radius is decreased to r/2 then tension in the string is
10N
20N
40N
5N
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the body in circular motion and apply the given conditions.
Step 1: Understand the initial conditions
We have a body of mass m revolving in a horizontal circle of radius r with a speed V. The tension in the string is given as T=10N.
Step 2: Apply the formula for tension in circular motion
The tension in the string provides the necessary centripetal force to keep the body moving in a circle. The formula for the tension T in terms of mass m, speed V, and radius r is given by:
T=mV2r
From the problem, we know that T=10N. Thus, we can write:
10=mV2r
Step 3: Analyze the new conditions
Now, the mass is increased to 2m and the radius is decreased to r2. We need to find the new tension T′ in the string while keeping the speed V constant.
Step 4: Write the new tension formula
Using the same formula for tension, we can express the new tension T′ as:
T′=(2m)V2r2
Step 5: Simplify the new tension formula
We can simplify the expression for T′:
T′=2mV2r2=2mV2⋅2r=4mV2r
Step 6: Substitute the value of mV2r
From Step 2, we know that mV2r=10. Therefore, we can substitute this into our equation for T′:
T′=4(mV2r)=4×10=40N
Final Answer
Thus, the tension in the string when the mass is increased to 2m and the radius is decreased to r2 is:
40N
We have a body of mass m revolving in a horizontal circle of radius r with a speed V. The tension in the string is given as T=10N.
The tension in the string provides the necessary centripetal force to keep the body moving in a circle. The formula for the tension T in terms of mass m, speed V, and radius r is given by:
T=mV2r
From the problem, we know that T=10N. Thus, we can write:
10=mV2r
Now, the mass is increased to 2m and the radius is decreased to r2. We need to find the new tension T′ in the string while keeping the speed V constant.
Using the same formula for tension, we can express the new tension T′ as:
T′=(2m)V2r2
We can simplify the expression for T′:
T′=2mV2r2=2mV2⋅2r=4mV2r
From Step 2, we know that mV2r=10. Therefore, we can substitute this into our equation for T′:
T′=4(mV2r)=4×10=40N
Thus, the tension in the string when the mass is increased to 2m and the radius is decreased to r2 is:
40N
Similar Questions
A body is made to revolve along a circle of radius r in horizontal plane at a time period T with the help of light horizontal string such that the tension in the string is F. If the radius of circle is increased to 2r and time period of revolution is decreased to T/2 then the tension in the string is
View SolutionA sphere of mass 300 grams is rotated at uniform angular velocity 2rads−1 along a circle of radius 1.25 m in horizontal plane with help of light horizontal string. The tension in the string is
View SolutionA stone of mass 0.3kg attched to a 1.5m long stirng is whirled around in a horizontal cirlcle at a speed of 6 m/s The tension in the string is
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
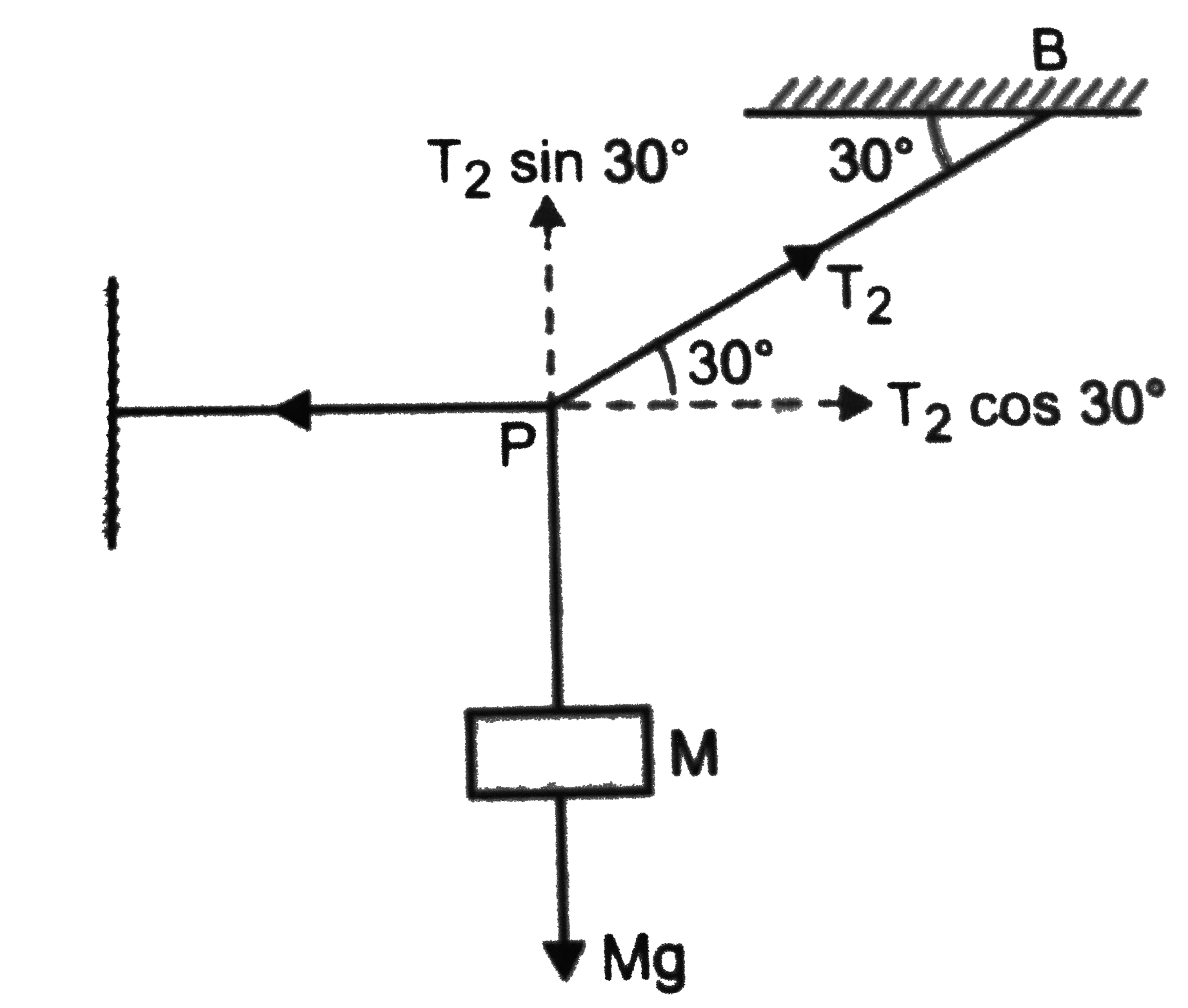
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
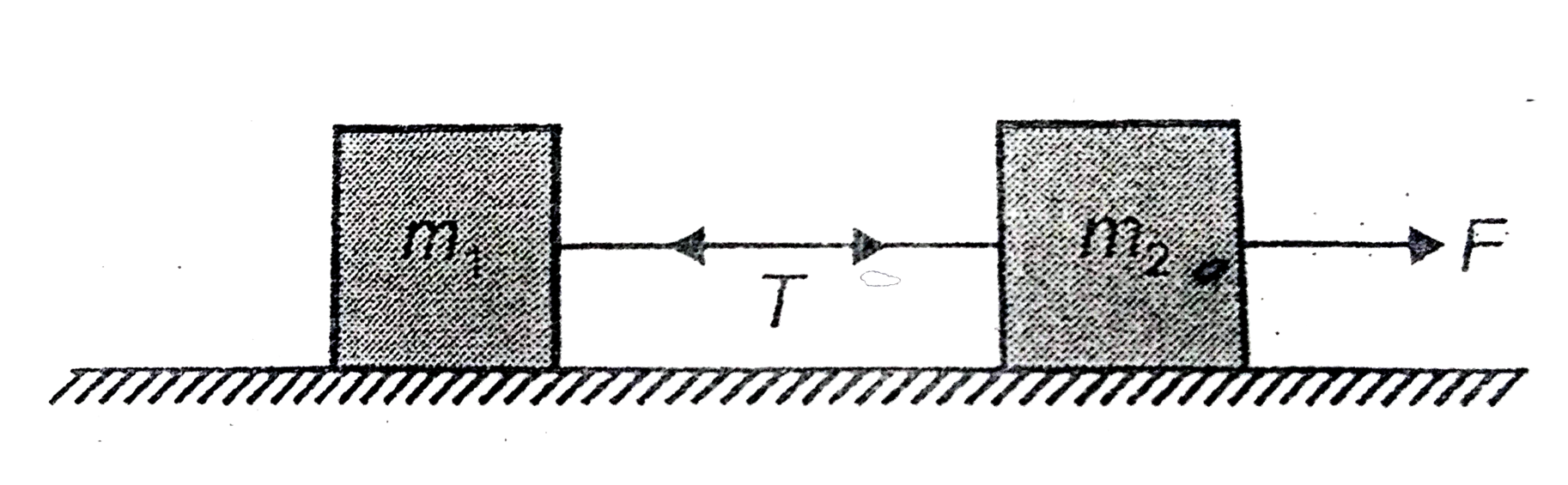
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionA stone of mass 0.1 kg tied to one end of a string lm long is revolved in a horizontal circle at the rate of 10π rev/s. Calculate the tension in the string.
View Solution
