A body is made to revolve along a circle of radius r in horizontal plane at a time period T with the help of light horizontal string such that the tension in the string is F. If the radius of circle is increased to 2r and time period of revolution is decreased to T/2 then the tension in the string is
F/2
2F
4F
8F
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the body revolving in a circular path and use the relationships between the radius, time period, and tension in the string.
Step 1: Understand the initial conditions
- The body is revolving in a circle of radius r with a time period T.
- The tension in the string is given as F.
Step 2: Relate tension to centripetal force
The tension F in the string provides the necessary centripetal force for circular motion. The formula for centripetal force Fc is given by:
Fc=m⋅ω2⋅r
where m is the mass of the body and ω is the angular velocity.
Step 3: Express angular velocity in terms of time period
The angular velocity ω can be expressed in terms of the time period T:
ω=2πT
Substituting this into the centripetal force equation gives:
F=m⋅(2πT)2⋅r
Step 4: Analyze the new conditions
Now, the radius is increased to 2r and the time period is decreased to T2. We need to find the new tension F′.
Step 5: Calculate the new angular velocity
The new angular velocity ω′ is:
ω′=2πT2=4πT
Step 6: Write the new centripetal force equation
The new centripetal force F′ is given by:
F′=m⋅ω′2⋅(2r)
Substituting for ω′:
F′=m⋅(4πT)2⋅(2r)
This simplifies to:
F′=m⋅16π2T2⋅(2r)=32⋅m⋅π2T2⋅r
Step 7: Relate the new tension to the original tension
From the original tension F=m⋅4π2T2⋅r, we can express F′ in terms of F:
F′=8⋅F
Conclusion
The tension in the string when the radius is increased to 2r and the time period is decreased to T2 is:
F′=8F
Final Answer
The tension in the string is 8F.
---
- The body is revolving in a circle of radius r with a time period T.
- The tension in the string is given as F.
The tension F in the string provides the necessary centripetal force for circular motion. The formula for centripetal force Fc is given by:
Fc=m⋅ω2⋅r
where m is the mass of the body and ω is the angular velocity.
The angular velocity ω can be expressed in terms of the time period T:
ω=2πT
Substituting this into the centripetal force equation gives:
F=m⋅(2πT)2⋅r
Now, the radius is increased to 2r and the time period is decreased to T2. We need to find the new tension F′.
The new angular velocity ω′ is:
ω′=2πT2=4πT
The new centripetal force F′ is given by:
F′=m⋅ω′2⋅(2r)
Substituting for ω′:
F′=m⋅(4πT)2⋅(2r)
This simplifies to:
F′=m⋅16π2T2⋅(2r)=32⋅m⋅π2T2⋅r
From the original tension F=m⋅4π2T2⋅r, we can express F′ in terms of F:
F′=8⋅F
The tension in the string when the radius is increased to 2r and the time period is decreased to T2 is:
F′=8F
The tension in the string is 8F.
Similar Questions
A body of mass m is made to revolve along a circle of radius r in horizontal plane at a speed Vm/s with help of light horizontal string such that the tension in the string is 10 N. Keeping speed constant if mass is increased to 2m und radius is decreased to r/2 then tension in the string is
View SolutionA sphere of mass 300 grams is rotated at uniform angular velocity 2rads−1 along a circle of radius 1.25 m in horizontal plane with help of light horizontal string. The tension in the string is
View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
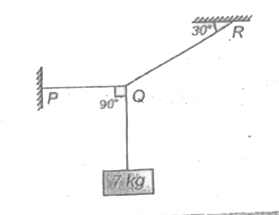
View SolutionA stone tied to the end of a string is whirled in a horizontal circle. The mass of the stone is 1.0 kg and the string is 0.50 m long. If the stone revolves at a constant speed for 10 times in 15.71 s, (a) what is the tension in the string? (b) What would happen to the tension in the string if the mass was doubled and all the other quantities remained the same? (c) What would happen to the tension in the string if the period was doubled and all the other quantities remain the same?
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionFor a particle rotating in a vertical circle with uniform speed, the maximum and minimum tension in the string are in the ratio 5 : 3. If the radius of vertical circle is 2 m, the speed of revolving body is (g=10m/s2)
View SolutionA stone of mass 0.1 kg tied to one end of a string lm long is revolved in a horizontal circle at the rate of 10π rev/s. Calculate the tension in the string.
View SolutionSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View Solution
