(A): Under given conditions of pressure and temperature, sound travels faster in a monoatomic gas than in diatomic gas.
(R): Opposition for wave to travel is more in diatomic gas than monoatomic gas.
Both 'A' and 'R' are true and 'R' is the correct, explanation of 'A'.
Both 'A' and 'R' are true and 'R' is not the correct explanation of 'A'
A' is true and 'R' is false
Both 'A' and 'R' are false
The correct Answer is:D
To solve the given assertion-reason question, we will analyze both statements step by step.
Step 1: Understanding the Assertion
The assertion states that under given conditions of pressure and temperature, sound travels faster in a monoatomic gas than in a diatomic gas.
- Explanation: The speed of sound in a gas is influenced by the molecular structure of the gas. Monoatomic gases (like helium or neon) consist of single atoms, while diatomic gases (like oxygen or nitrogen) consist of molecules made up of two atoms.
Step 2: Understanding the Reason
The reason states that the opposition for a wave to travel is more in diatomic gas than in monoatomic gas.
- Explanation: The opposition to sound waves traveling through a medium can be related to the specific heat capacities of the gas. The adiabatic constant (γ = Cp/Cv) plays a crucial role in determining the speed of sound.
Step 3: Relating the Concepts
The speed of sound in a gas can be expressed as:
v=√γ⋅Pρ
where:
- v is the speed of sound,
- γ is the adiabatic constant,
- P is the pressure,
- ρ is the density of the gas.
For monoatomic gases, γ is approximately 1.66, while for diatomic gases, γ is approximately 1.4.
Step 4: Comparing the Speeds
Since γ for monoatomic gases is greater than that for diatomic gases, the speed of sound in monoatomic gases will be greater than in diatomic gases when pressure and density are constant.
Conclusion
Thus, the assertion is true: sound travels faster in monoatomic gases than in diatomic gases. However, the reason provided is not a valid explanation for the assertion, making it false.
Final Answer
- Assertion (A): True
- Reason (R): False
The assertion states that under given conditions of pressure and temperature, sound travels faster in a monoatomic gas than in a diatomic gas.
The reason states that the opposition for a wave to travel is more in diatomic gas than in monoatomic gas.
The speed of sound in a gas can be expressed as:
v=√γ⋅Pρ
where:
- v is the speed of sound,
- γ is the adiabatic constant,
- P is the pressure,
- ρ is the density of the gas.
Since γ for monoatomic gases is greater than that for diatomic gases, the speed of sound in monoatomic gases will be greater than in diatomic gases when pressure and density are constant.
Thus, the assertion is true: sound travels faster in monoatomic gases than in diatomic gases. However, the reason provided is not a valid explanation for the assertion, making it false.
- Assertion (A): True
- Reason (R): False
Topper's Solved these Questions
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Wave Equations & Basics :)
Explore 19 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-II (Strings (Speed of a travelling wave:))
Explore 23 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-IA (Matching )
Explore 4 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:PROBLEMS (LEVEL - II)
Explore 33 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -III (POLARISITION)
Explore 10 Videos
Similar Questions
Knowledge Check
In an adiabatic change the pressure and temperature of monoatomic gas are related as P∝Tc where C equal
A2/5B5/2C3/5D5/3
What is the degree of freedom in case of a monoatomic gas?
View SolutionHeat capacity of a diatomic gas is higher than that of a monoatomic gas.
View SolutionFor one mole of a monoatomic gas match the following.
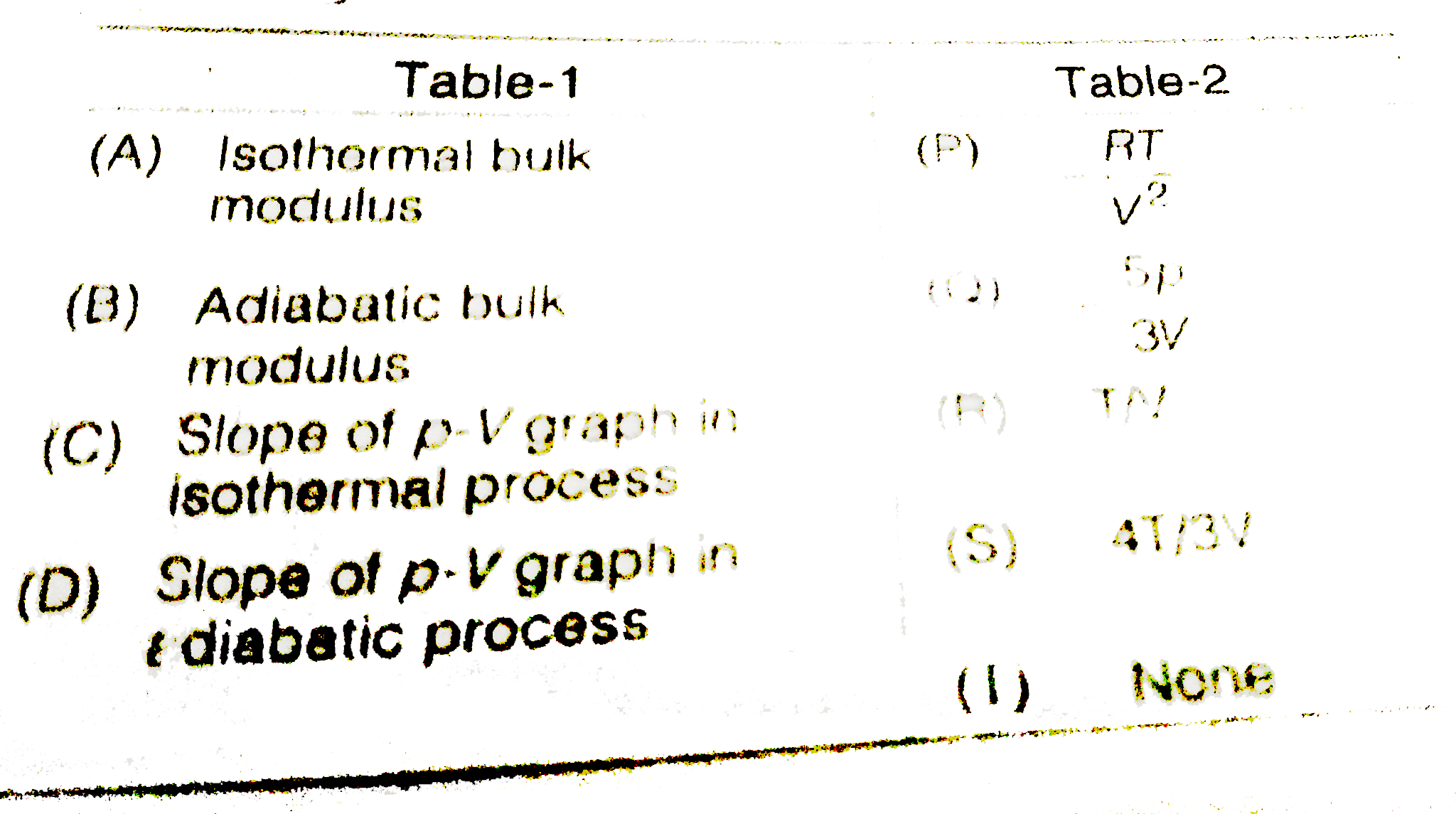
View SolutionThe ratio of the specific heat at constant pressure to that at constant volume is larger for a diatomic gas than for a monoatomic gas.
View SolutionThe heat capacity of a diatomic gas is higher than that of a monatomic gas.
View SolutionGraph for specific heat at constant volume for a monoatomic gas
View SolutionGraph for specific heat at constant volume for a monoatomic gas
View Solution
