Calculate the impact parameter of a 5 MeV particle scattered by 90∘ when it approaches a gold nucleus.
15.27x10−14 m
23.23×10−14 m
2.27×10−14m
77.2×10−14m
The correct Answer is:C
To calculate the impact parameter of a 5 MeV particle scattered by 90∘ when it approaches a gold nucleus, we can follow these steps:
Step 1: Understand the Problem
The impact parameter b is the perpendicular distance from the center of the nucleus to the path of the incoming particle if it were to continue in a straight line. The particle is an alpha particle with an energy of 5 MeV, and it scatters at an angle of 90∘.
Step 2: Relevant Formula
The impact parameter can be calculated using the formula:
b=Z1Z2e2cot(θ/2)4πϵ0E
where:
- Z1 is the atomic number of the alpha particle (which is 2 for helium),
- Z2 is the atomic number of the gold nucleus (which is 79),
- e is the charge of the electron (1.6×10−19C),
- ϵ0 is the permittivity of free space (8.85×10−12C2/N m2),
- E is the energy of the alpha particle in joules,
- θ is the scattering angle.
Step 3: Convert Energy to Joules
The energy of the alpha particle is given as 5 MeV. To convert this to joules:
E=5MeV=5×1.6×10−13J=8×10−13J
Step 4: Calculate cot(θ/2)
For a scattering angle of 90∘:
θ=90∘⟹cot(θ/2)=cot(45∘)=1
Step 5: Substitute Values into the Formula
Now substituting the values into the impact parameter formula:
b=(2)(79)(1.6×10−19)2⋅14π(8.85×10−12)(8×10−13)
Step 6: Calculate the Numerator
Calculating the numerator:
(2)(79)(1.6×10−19)2=2×79×2.56×10−38=404.48×10−38=4.0448×10−36
Step 7: Calculate the Denominator
Calculating the denominator:
4π(8.85×10−12)(8×10−13)≈4×3.14×8.85×10−12×8×10−13≈8.84×10−24
Step 8: Final Calculation
Now, substituting the values back into the impact parameter equation:
b=4.0448×10−368.84×10−24≈4.57×10−13m
Step 9: Conclusion
Thus, the impact parameter b is approximately 4.57×10−13m.
The impact parameter b is the perpendicular distance from the center of the nucleus to the path of the incoming particle if it were to continue in a straight line. The particle is an alpha particle with an energy of 5 MeV, and it scatters at an angle of 90∘.
The impact parameter can be calculated using the formula:
b=Z1Z2e2cot(θ/2)4πϵ0E
where:
- Z1 is the atomic number of the alpha particle (which is 2 for helium),
- Z2 is the atomic number of the gold nucleus (which is 79),
- e is the charge of the electron (1.6×10−19C),
- ϵ0 is the permittivity of free space (8.85×10−12C2/N m2),
- E is the energy of the alpha particle in joules,
- θ is the scattering angle.
The energy of the alpha particle is given as 5 MeV. To convert this to joules:
E=5MeV=5×1.6×10−13J=8×10−13J
For a scattering angle of 90∘:
θ=90∘⟹cot(θ/2)=cot(45∘)=1
Now substituting the values into the impact parameter formula:
b=(2)(79)(1.6×10−19)2⋅14π(8.85×10−12)(8×10−13)
Calculating the numerator:
(2)(79)(1.6×10−19)2=2×79×2.56×10−38=404.48×10−38=4.0448×10−36
Calculating the denominator:
4π(8.85×10−12)(8×10−13)≈4×3.14×8.85×10−12×8×10−13≈8.84×10−24
Now, substituting the values back into the impact parameter equation:
b=4.0448×10−368.84×10−24≈4.57×10−13m
Thus, the impact parameter b is approximately 4.57×10−13m.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PROBLEM24videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE - I20videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE -II35videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (ADVANCED) (Integer Type Questions)2videos
CAPACITORS
Similar Questions
Knowledge Check
- Question 1 - Select One
The impact parameter at which the scattering angle is 900,z=79 and initial energy 10MeV is
A1.137*10^-14B1.137*10^-16C2.24*10^-17Dzero - Question 2 - Select One
For scattering by an inverse-square field (such as that produced by a charged nucleus in Rutherford's model) the relation between impact parameter b and the scattering angle θ is given by, the scattering angle for b=0 is
A180∘B90∘C45∘D120∘ - Question 3 - Select One
(A) the trajetory traced by an incident particle depends on the impact parameter of collision.
(R) the impact parameter is the perpendicular distance of the initial velocity vector of the incident particle from the centre of the target nucleus.Aif both assertion and reason are true and reason is the correct explanation of assertion.Bif both assertion and reason are true but reason is not the correct explanation of assertion.Cif assertion is true but reason is false.Dif both assertion and reason are false.
In Rutherford's experiment, number of particles scattered at 90∘ angel are x per second. Number particles scattered per second at angle 60∘ is
View SolutionFor scattering by an inverse square field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle θ is given by,
b=Ze2cotθ/24πε0(12mv2)
What is the impact parameter at which the scattering angle is 90∘ for Z = 79 and initial energy equal to 10MeV ?View SolutionWhen a silver foil (Z = 47) was used in an α ray scattering experiment , the number of α-particles scattered at 30∘ was found to be 200 per minute. If the silver foil is replaced by alumninium (z = 13) foil of same thickness, the number of α-particles scattered per minute at 30∘ is nearly equal to
View SolutionIn Rutherford experiments on α-ray scattering the number of particles scattered at 900angle be 28 per minute. Then the number of particles scattered per minute by the same foil, but at 600 is
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
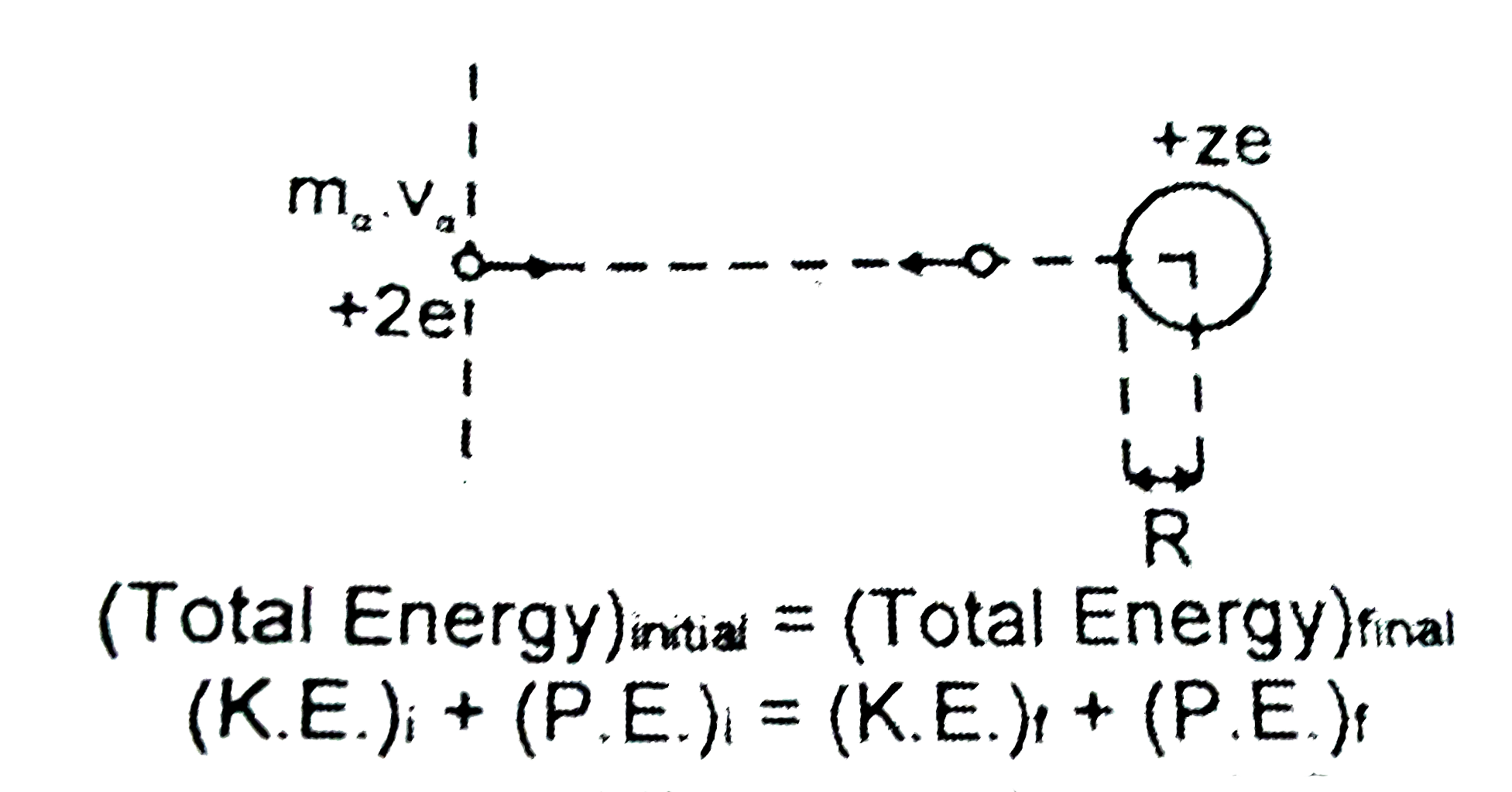
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :View Solution

