When n number of particles each of mass m are at distances x1=1,x2=2,x3=3,……….,xn=n units from origin on the x-axis, then find the distance of their centre of mass from origin.
To find the distance of the center of mass of n particles, each of mass m, located at distances x1=1,x2=2,x3=3,...,xn=n from the origin on the x-axis, we can follow these steps:
Step 1: Understand the Position of Each Particle
Each particle is located at a distance from the origin on the x-axis. The positions are:
- Particle 1: \( x_1 = 1 \)
- Particle 2: \( x_2 = 2 \)
- Particle 3: \( x_3 = 3 \)
- ...
- Particle n: \( x_n = n \)
Step 2: Write the Formula for Center of Mass
The formula for the center of mass \( x_{cm} \) of a system of particles is given by:
\(
x_{cm} = \frac{\sum (m_i \cdot x_i)}{\sum m_i}
\)
where \( m_i \) is the mass of each particle and \( x_i \) is the position of each particle.
Step 3: Calculate the Total Mass
Since each particle has the same mass \( m \), the total mass \( M \) of the system is:
\(
M = m + m + m + ... + m \quad (n \text{ times}) = n \cdot m
\)
Step 4: Calculate the Weighted Sum of Positions
Now, we need to calculate the sum of the products of mass and position:
\(
\sum (m_i \cdot x_i) = m \cdot x_1 + m \cdot x_2 + m \cdot x_3 + ... + m \cdot x_n
\)
This simplifies to:
\(
\sum (m_i \cdot x_i) = m \cdot (1 + 2 + 3 + ... + n)
\)
The sum of the first n natural numbers is given by the formula:
\(
1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}
\)
Thus,
\(
\sum (m_i \cdot x_i) = m \cdot \frac{n(n + 1)}{2}
\)
Step 5: Substitute into the Center of Mass Formula
Now we can substitute the values into the center of mass formula:
\(
x_{cm} = \frac{m \cdot \frac{n(n + 1)}{2}}{n \cdot m}
\)
The mass \( m \) cancels out:
\(
x_{cm} = \frac{\frac{n(n + 1)}{2}}{n}
\)
This simplifies to:
\(
x_{cm} = \frac{n + 1}{2}
\)
Final Answer
Thus, the distance of the center of mass from the origin is:
\(
\boxed{\frac{n + 1}{2}}
\)
Each particle is located at a distance from the origin on the x-axis. The positions are:
- Particle 1: \( x_1 = 1 \)
- Particle 2: \( x_2 = 2 \)
- Particle 3: \( x_3 = 3 \)
- ...
- Particle n: \( x_n = n \)
The formula for the center of mass \( x_{cm} \) of a system of particles is given by:
\(
x_{cm} = \frac{\sum (m_i \cdot x_i)}{\sum m_i}
\)
where \( m_i \) is the mass of each particle and \( x_i \) is the position of each particle.
Since each particle has the same mass \( m \), the total mass \( M \) of the system is:
\(
M = m + m + m + ... + m \quad (n \text{ times}) = n \cdot m
\)
Now, we need to calculate the sum of the products of mass and position:
\(
\sum (m_i \cdot x_i) = m \cdot x_1 + m \cdot x_2 + m \cdot x_3 + ... + m \cdot x_n
\)
This simplifies to:
\(
\sum (m_i \cdot x_i) = m \cdot (1 + 2 + 3 + ... + n)
\)
The sum of the first n natural numbers is given by the formula:
\(
1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}
\)
Thus,
\(
\sum (m_i \cdot x_i) = m \cdot \frac{n(n + 1)}{2}
\)
Now we can substitute the values into the center of mass formula:
\(
x_{cm} = \frac{m \cdot \frac{n(n + 1)}{2}}{n \cdot m}
\)
The mass \( m \) cancels out:
\(
x_{cm} = \frac{\frac{n(n + 1)}{2}}{n}
\)
This simplifies to:
\(
x_{cm} = \frac{n + 1}{2}
\)
Thus, the distance of the center of mass from the origin is:
\(
\boxed{\frac{n + 1}{2}}
\)
Similar Questions
When n number of particles each of mass m are at distances x1=a,x2=ar,x3=ar2…….xn=arn units from origin on the x-axis, then the distance of their centre of mass from origin.
View SolutionWhen .n. number of particles of masses m, 2m, 3m, …….. nm are at distances x1=1,x2=2,x3=3,……………xn=n units respectively from origin on the x-axis, then find the distance of centre of mass of the system from origin.
View SolutionWhen n number of particles of masses m,2m,3m,……..nm are at distances x1=1,x2=4,x3=9,………xn=n2 units respectively from origin on the x-axis, then find the distance of their centre of mass from origin.
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionFind the points of the x-axis, whose distances from the line x3+y4=1are 4 unit is.
View SolutionThe sum of deviations of a set of values x1,x2,x3,……xn measured from 50 is -10 and the sum of deviations of the values from 46 is 70. Find the value of n and the mean.
View SolutionAll the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is
View SolutionThe average of n numbers x1,x2,x3,..,xn is M. If xn is replaced by x', then new average is
View SolutionWe know that when two equal masses are placed on a line then, gravitational force on a third mass is zero due to these two masses when the third is placed at the centre of line joining the two masses. But if third mass is placed anywhere else on the x-axis, the gravitational force acts on that mass due to these two masses. Consider a system shown in figure.
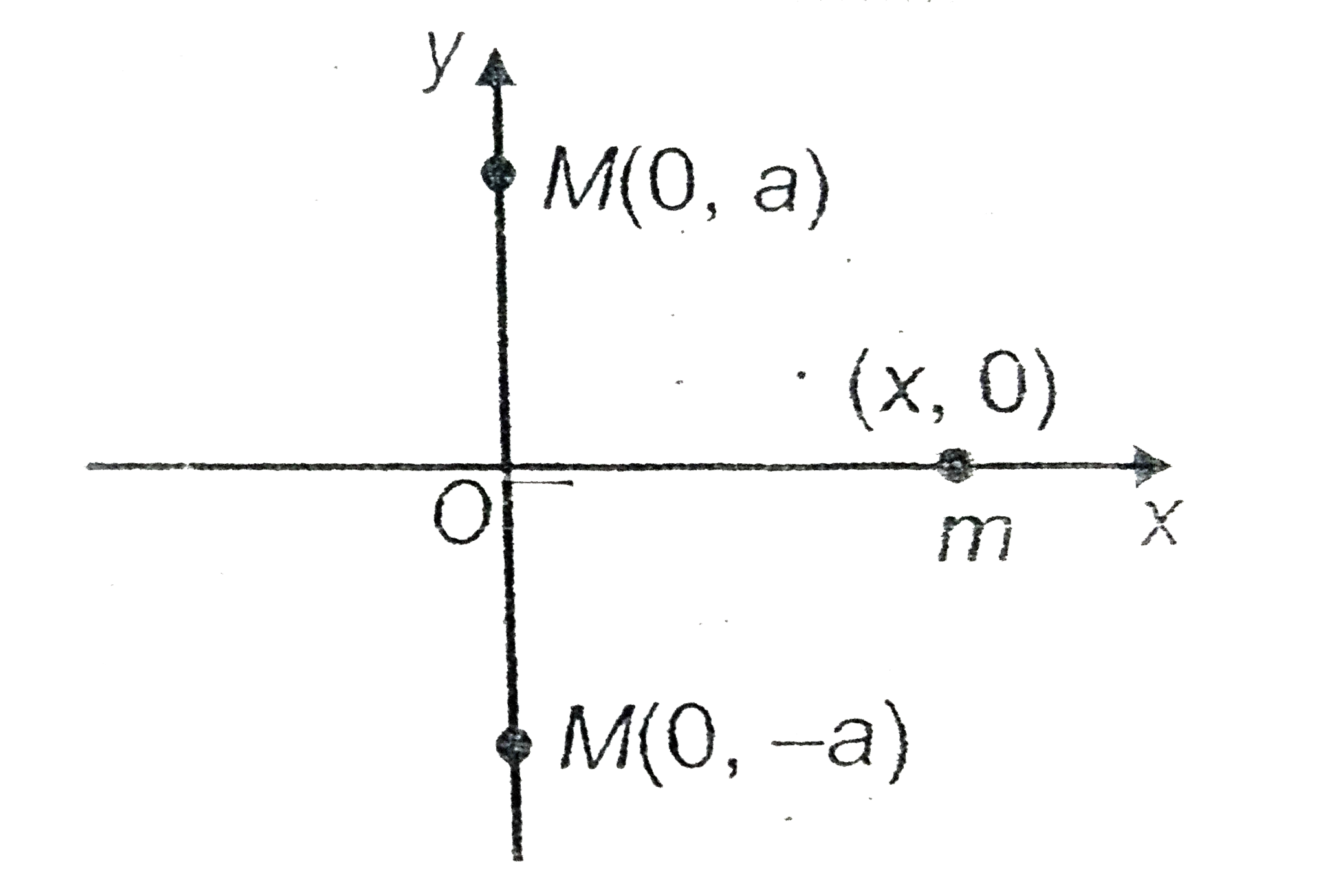
In this system two point masses of mass M each are placed at y-axis at a distance a from origin and these masses are fixed. If a third point mass of mass m is released at a distance x from origin on x-axis, then answer the following questions.
The distance between positions of maximum force on mass m is
View SolutionA large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View Solution