Four transparent slabs having thickness t1=2cm,t2=4cm,t3=3cm and t4=5cm are introduced in one of the paths of light emitted by two narrow slits the ascending order of shift of the central fringe
t1,t2,t3,t4
t4,t3,t2,t1
t3,t2,t4,t1
t1,t3,t2,t4
The correct Answer is:D
To find the ascending order of shift of the central fringe caused by four transparent slabs of different thicknesses, we can follow these steps:
1. Identify the Thicknesses of the Slabs:
- The thicknesses of the slabs are given as:
- t1=2cm
- t2=4cm
- t3=3cm
- t4=5cm
2. Understand the Relationship Between Thickness and Fringe Shift:
- The shift in the central fringe (Δt) due to a slab is directly proportional to its thickness. The formula can be simplified to:
Δt∝t
- This means that the larger the thickness of the slab, the greater the shift in the fringe.
3. Arrange the Thicknesses in Ascending Order:
- We will now arrange the thicknesses from smallest to largest:
- t1=2cm
- t3=3cm
- t2=4cm
- t4=5cm
4. Determine the Order of Shift:
- Based on the thicknesses, the order of shift of the central fringe will be:
- First: t1 (2 cm)
- Second: t3 (3 cm)
- Third: t2 (4 cm)
- Fourth: t4 (5 cm)
5. Final Ascending Order of Shift:
- Therefore, the ascending order of shift of the central fringe due to the slabs is:
t1<t3<t2<t4
Conclusion:
The ascending order of shift of the central fringe is:
- t1(2cm)<t3(3cm)<t2(4cm)<t4(5cm)
- The thicknesses of the slabs are given as:
- t1=2cm
- t2=4cm
- t3=3cm
- t4=5cm
- The shift in the central fringe (Δt) due to a slab is directly proportional to its thickness. The formula can be simplified to:
Δt∝t
- This means that the larger the thickness of the slab, the greater the shift in the fringe.
- We will now arrange the thicknesses from smallest to largest:
- t1=2cm
- t3=3cm
- t2=4cm
- t4=5cm
- Based on the thicknesses, the order of shift of the central fringe will be:
- First: t1 (2 cm)
- Second: t3 (3 cm)
- Third: t2 (4 cm)
- Fourth: t4 (5 cm)
- Therefore, the ascending order of shift of the central fringe due to the slabs is:
t1<t3<t2<t4
The ascending order of shift of the central fringe is:
- t1(2cm)<t3(3cm)<t2(4cm)<t4(5cm)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IB (ASSERTION AND REASON)67videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (INTERFERENCE)26videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (MATCHING TYPE QUESTIONS)6videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
The n transparent slabs of refractive index1.5 each having thickness 1cm, 2 cm,…to n cm are arranged one over another. A point object is seen through this combineation with near perpendicular light. If the shift of object by the combination is 1 cm, then find the value of n.
View SolutionIn YDSE with d=1mm and D=1m, Slabs of (t=1μm,μ=3) and (t=0.5μm,μ=2) are introduced in front of upper and lower slits, respectively. Find the shift in the fringe pattern.
View SolutionLight of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?View SolutionA ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionIn the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2μ and μ respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N.
[d=1mm,D=1m,t=2×10−2mm,μ=32]
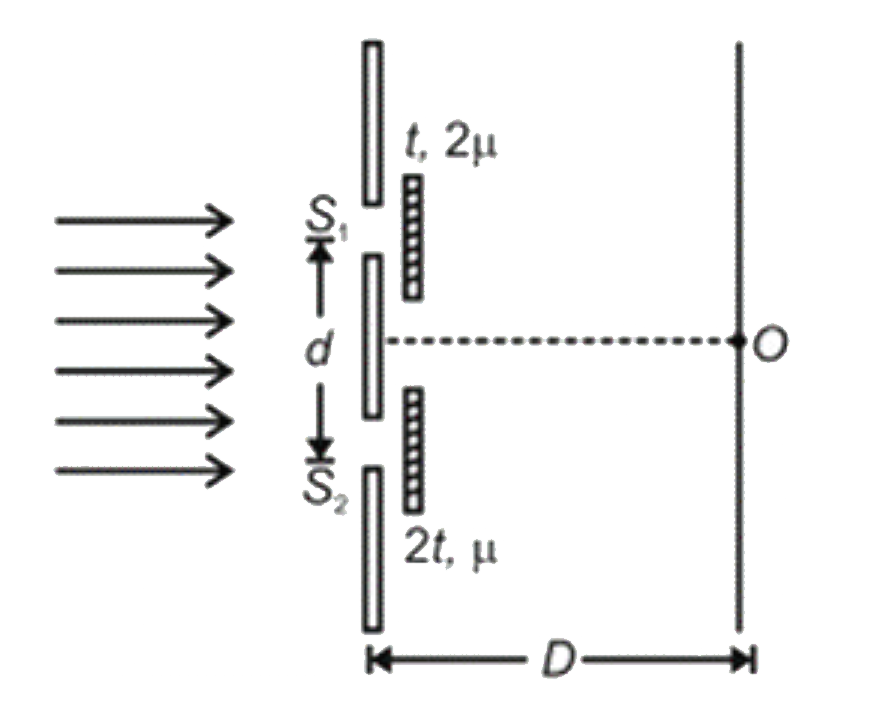 View Solution
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe. The intensity at a distance x=4×10−5in form the central maximum is-
View SolutionIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright fringe gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be (symbols have their usual meaning )
View SolutionThe slits in a double-slit interference experiment are illuminated by orange light (λ=60nm). A thin transparent plastic of thickness t is placed in front of one of the slits. The nunber of fringes shifting on screen is plotted versus the refractive index μ of the plastic in graph shown in figure. The value of t is
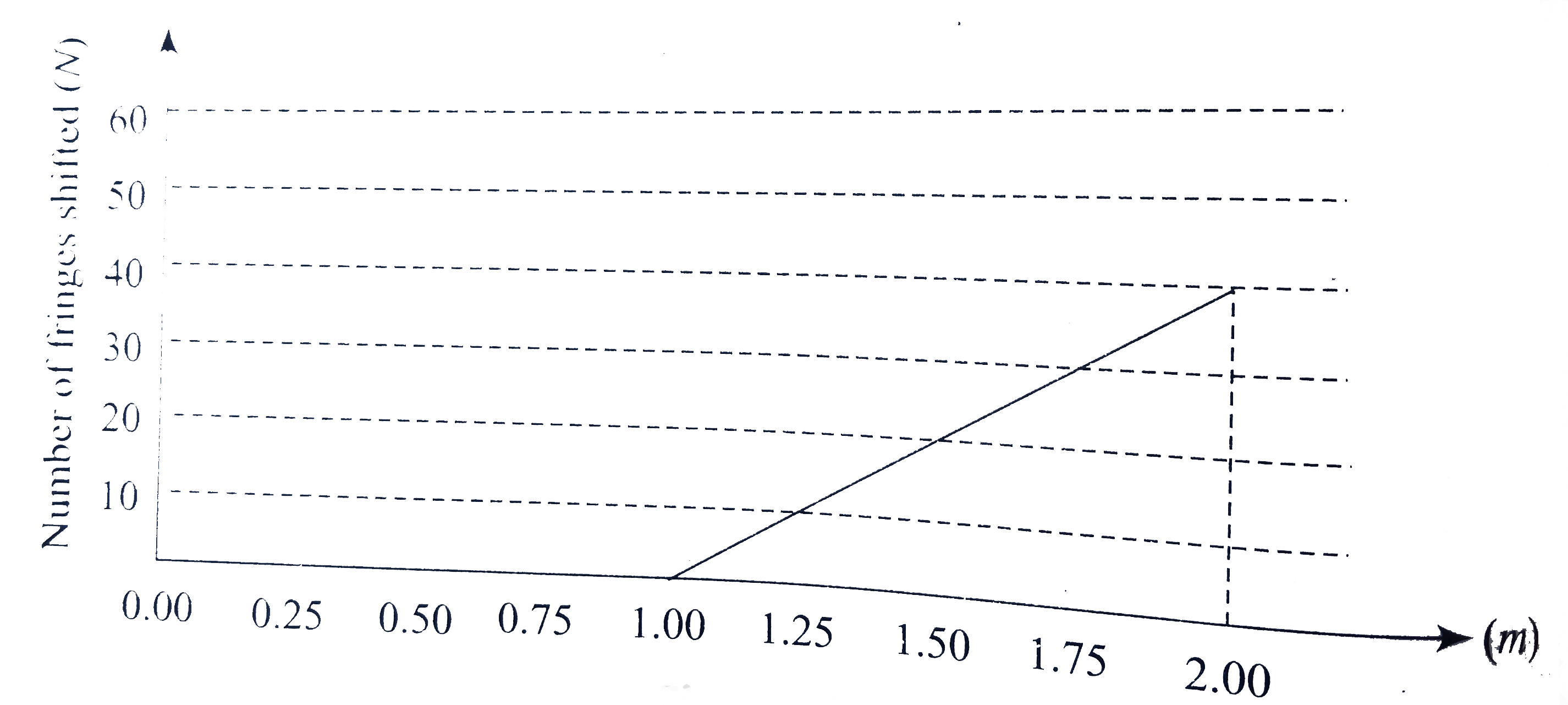 View Solution
View SolutionIn YDSE, a glass slab of refractive index, μ=1.5 and thickness 'l' is introduced in one of the interfening beams of wavelength λ=5000A. If on introducing the slab, the central fringe shift by 2 mm, then thickness of stab would be (Fringe width, β=0.2mm)
View Solution

