A : In Y.D.S.E., if distance of screen (D) is very large compared to the fringe width, the fringes will be very nearly straight lies.
R : In general, the shape of fringes formed in Y.D.S.E is hyperbola.
Both A and R are true and R is the correct explanation of A
Both A and R are true and R is not the correct explanation of A
A is true and R is false
Both A and R are false
The correct Answer is:B
To analyze the statements A and R regarding Young's Double Slit Experiment (Y.D.S.E.), let's break down the concepts step by step.
Step 1: Understanding the Fringe Formation in Y.D.S.E.
In Y.D.S.E., when light passes through two slits, it creates an interference pattern on a screen. The pattern consists of alternating bright and dark fringes.
Hint: The interference pattern is a result of constructive and destructive interference of light waves from the two slits.
Step 2: Analyzing Statement A
Statement A claims that if the distance of the screen (D) is very large compared to the fringe width (β), the fringes will appear as nearly straight lines.
- When D is much larger than the fringe width, the angle θ (the angle between the central maximum and the nth fringe) becomes very small.
- For small angles, sin(θ) ≈ tan(θ) ≈ θ, which means that the path difference becomes negligible, and the fringes appear straight.
Hint: Consider the geometry of the setup and how angles change with distance.
Step 3: Analyzing Statement R
Statement R states that the shape of the fringes formed in Y.D.S.E. is generally a hyperbola.
- The fringes can be described mathematically. The condition for constructive interference (bright fringes) is given by the equation:
dsin(θ)=nλ
where d is the distance between the slits, n is an integer, and λ is the wavelength of light.
- When plotted, the locus of points that satisfy this condition can resemble a hyperbola, especially when considering the difference in distances from the two slits to a point on the screen.
Hint: Recall the definition of a hyperbola and how it relates to the interference conditions.
Step 4: Conclusion
Both statements A and R are true. Statement A is true because a large D relative to fringe width results in nearly straight fringes. Statement R is also true because the mathematical representation of the fringe pattern can be described as hyperbolic.
Final Answer
Both statements A and R are true, and the correct option is that both are true.
In Y.D.S.E., when light passes through two slits, it creates an interference pattern on a screen. The pattern consists of alternating bright and dark fringes.
Statement A claims that if the distance of the screen (D) is very large compared to the fringe width (β), the fringes will appear as nearly straight lines.
- For small angles, sin(θ) ≈ tan(θ) ≈ θ, which means that the path difference becomes negligible, and the fringes appear straight.
Statement R states that the shape of the fringes formed in Y.D.S.E. is generally a hyperbola.
dsin(θ)=nλ
where d is the distance between the slits, n is an integer, and λ is the wavelength of light.
- When plotted, the locus of points that satisfy this condition can resemble a hyperbola, especially when considering the difference in distances from the two slits to a point on the screen.
Both statements A and R are true. Statement A is true because a large D relative to fringe width results in nearly straight fringes. Statement R is also true because the mathematical representation of the fringe pattern can be described as hyperbolic.
Both statements A and R are true, and the correct option is that both are true.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (INTERFERENCE)26videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (DIFFRACTION)17videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (ASCENDING AND DSCENDING ORDER TYPE QUESTIONS)6videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
If S1andS2 are two point sources emitting light in phase , then what is the shape of interference fringes formed on the screen ?
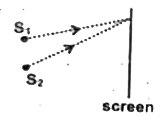View SolutionIn a YDSE experiment, the distance between the slits & the screen is 100cm. For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25mm. When the distance between the slits is increased by Δd=1.2mm, the fringe width decreased to n=2/3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light.
View SolutionIf white light is used in Young's double -slit experiment
a) bright white fringe is formed at the centre of the screen
b) fringes of different colours are observed on both sides of central fringe clearly only in the first order
c) the first order violet fringes are closer to the centre of the screen than the first order red fringes
d) the first order red fringes are closer to the centre of the screen than the first order violet fringesView Solution(i) Write two points to distinguish between interference and diffraction fringes.
(ii) In a Young 's double slit experiment , fringes are obtained on a screen placed at certain distance away from the slits . If the screen is moved by 5 cm towards the slits , the fringe width changes by 30 μm . Given that the slits are 1 mm apart , calculate the wavelength of the light used.View SolutionThe minimum value of d os that there is a dark fringe at O is dmin. For the value of dmin, the distance at which the next bright fringe is formed is x. Then
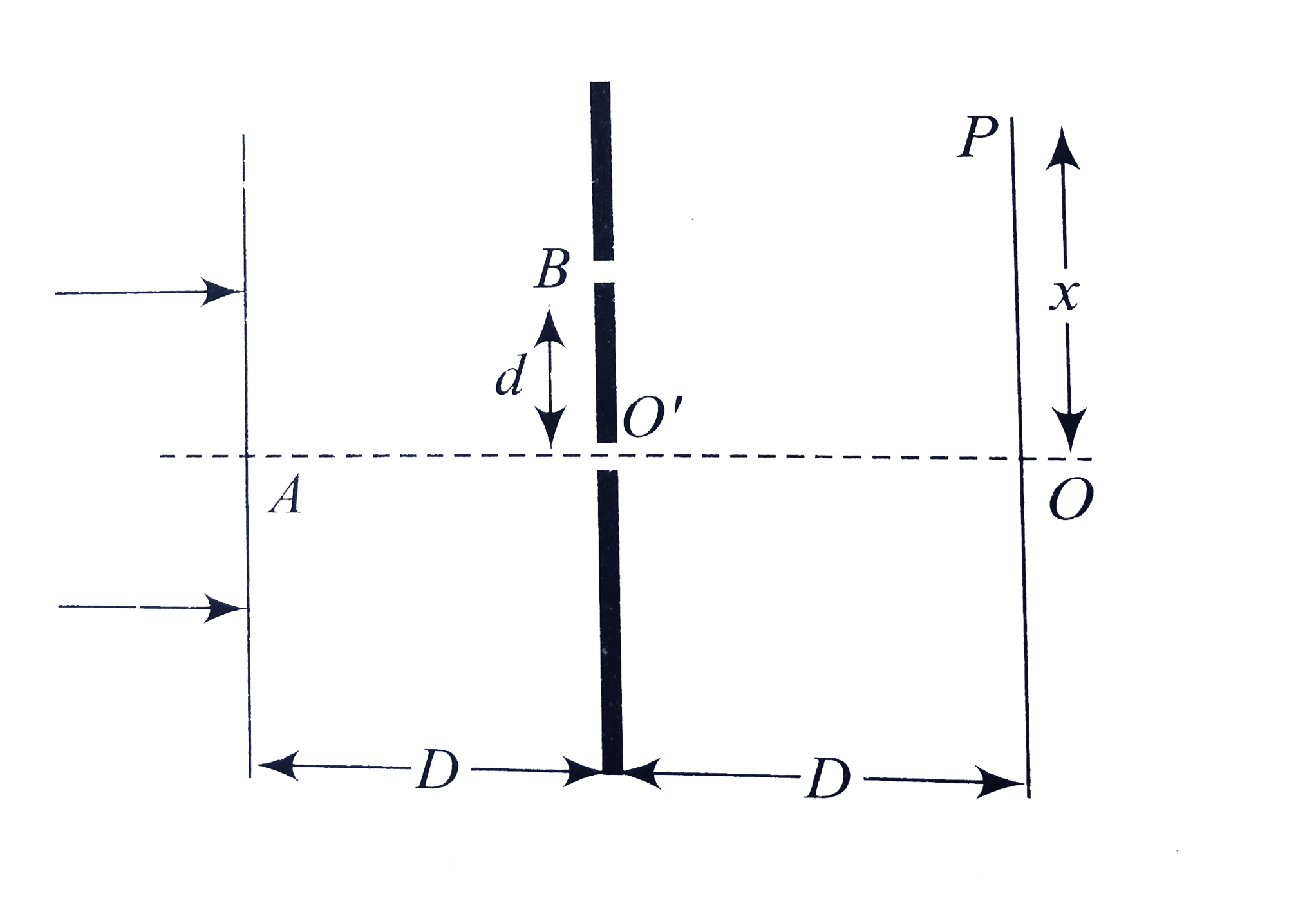View SolutionA particle is placed on the top of a hemispherical shell of same mass. Shell is free to move on the smooth ground. If particle is given a given a gentle push and reaches to angular position q as shown in figure then for an observer fixed on a shell, ratio of reaction force exerted by shell to pseudo force (as observed from shell) acting on particle, is
View SolutionIn YDSE the distance between the slits is 1mm and screen is 25nm away from intensities IF the wavelength of light is 6000A the fringe width on the screen is
View SolutionRed light I(λ=664nm in vacuum) is used in Young's experiment with the slits separated by a distance from the screen given by D=2.75m. Find the distance y on the screen between the central bright fringe and the third-order bright fringe.
Reasoning: This problem can be solved by the first using Eq. (i) to determine the value of θ that locates the third-order bright fringe. Then, trigonometry can be used to obatin the distance y.View SolutionIn a Young's double slit experiment with light of wavelength λ the separation of slits is d and distance of screen is D such that D>>d>>λ. If the fringe width is bea, the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is
View SolutionIn a standard YDSE slit width is 1mm and distance of screen from the slit is 1m. If wavelength of light is 632nm and bright fringe formed at y = 1.270 mm. Find path difference for the point
View Solution