An electromagnetic wave emitted by source travels 21 km to arrive at a receiver. The wave while travelling in another path is reflected from a surface at 19 km away and further travels 12 km to reach the same receiver. If destructive interference occurs at the receiving end, the mximum wavelength of the wave is
0.5km
1km
5km
10km
The correct Answer is:D
To solve the problem, we need to determine the maximum wavelength of the electromagnetic wave that results in destructive interference at the receiver. Here are the steps to arrive at the solution:
Step 1: Identify the paths of the electromagnetic wave
- The first path (X1) is the direct path from the source to the receiver, which is given as 21 km.
- The second path (X2) involves the wave being reflected from a surface. The distance to the reflecting surface is 19 km, and then it travels an additional 12 km to reach the receiver.
Step 2: Calculate the total distance for the second path
- The total distance for the second path (X2) can be calculated as:
X2=19 km+12 km=31 km
Step 3: Determine the path difference
- The path difference (ΔX) between the two paths is given by:
ΔX=X2−X1=31 km−21 km=10 km
Step 4: Apply the condition for destructive interference
- The condition for destructive interference is modified when one of the waves is reflected. The modified condition is:
λm=ΔX
where m is an integer (0, 1, 2, ...).
Step 5: Find the maximum wavelength
- To find the maximum wavelength (λ_max), we can set m=1 (the first order of destructive interference):
λmax=ΔX=10 km
Conclusion
- The maximum wavelength of the wave that results in destructive interference at the receiving end is 10 kilometers.
- The first path (X1) is the direct path from the source to the receiver, which is given as 21 km.
- The second path (X2) involves the wave being reflected from a surface. The distance to the reflecting surface is 19 km, and then it travels an additional 12 km to reach the receiver.
- The total distance for the second path (X2) can be calculated as:
X2=19 km+12 km=31 km
- The path difference (ΔX) between the two paths is given by:
ΔX=X2−X1=31 km−21 km=10 km
- The condition for destructive interference is modified when one of the waves is reflected. The modified condition is:
λm=ΔX
where m is an integer (0, 1, 2, ...).
- To find the maximum wavelength (λ_max), we can set m=1 (the first order of destructive interference):
λmax=ΔX=10 km
- The maximum wavelength of the wave that results in destructive interference at the receiving end is 10 kilometers.
Topper's Solved these Questions
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (DIFFRACTION)
17 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (POLARISATION)
10 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IB (ASSERTION AND REASON)
67 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
A sound source emits two sinusoidal sound waves, both of wavelength λ, along paths A and B as shown in figure.The sound travelling along path B is reflected from five surfaces as shown and then merges at point Q, producing minimum intensity at that point.The minimum value of d in terms of λ is :

View SolutionA narrow tube is bent in the form of a circle of radius R, as shown in figure. Two small holes S and D are made in the tube at the position at right angle to each other. A source placed at S generates a wave of intensity I0 which two parts: one part travels along the longer path, while the other travels along the shorter path. Both the waves meet at point D where a detector is placed.

2. If a minima is formed at the detector, then the magnitude of wavelength λ of the wave produced is given by
View Solution
Knowledge Check
Assertion: Space waves are used for line -of -sight communication.
Reason: Space wave travels in a straight line from transmitting antenna to the receiving antenna.AA and R both are true and R is correct explaination of ABA is true but R is falseCA is false but R is trueDBoth are false
In a large room , a person receives direct sound waves from a source 120 metres away from him. He also receives waves from the same source which reach , being reflected from the 25m high ceiling at a point halfway between them . The two waves interfere constructively for a wavelength of
View SolutionIn a hall, a person receives direct sound waves from a source 120m away. He also receives waves from the same source which reach him after being reflected from the 25m high ceiling at a point halfway between them. The two waves interfere constructively for wavelengths (in metres)
View SolutionA narrow tube is bent in the form of a circle of radius R, as shown in figure. Two small holes S and D are made in the tube at the position at right angle to each other. A source placed at S generates a wave of intensity I0 which two parts: one part travels along the longer path, while the other travels along the shorter path. Both the waves meet at point D where a detector is placed.

1. If a maxima if formed at a detector, then the magnitude of wavelength λ of the, wave produced is given by
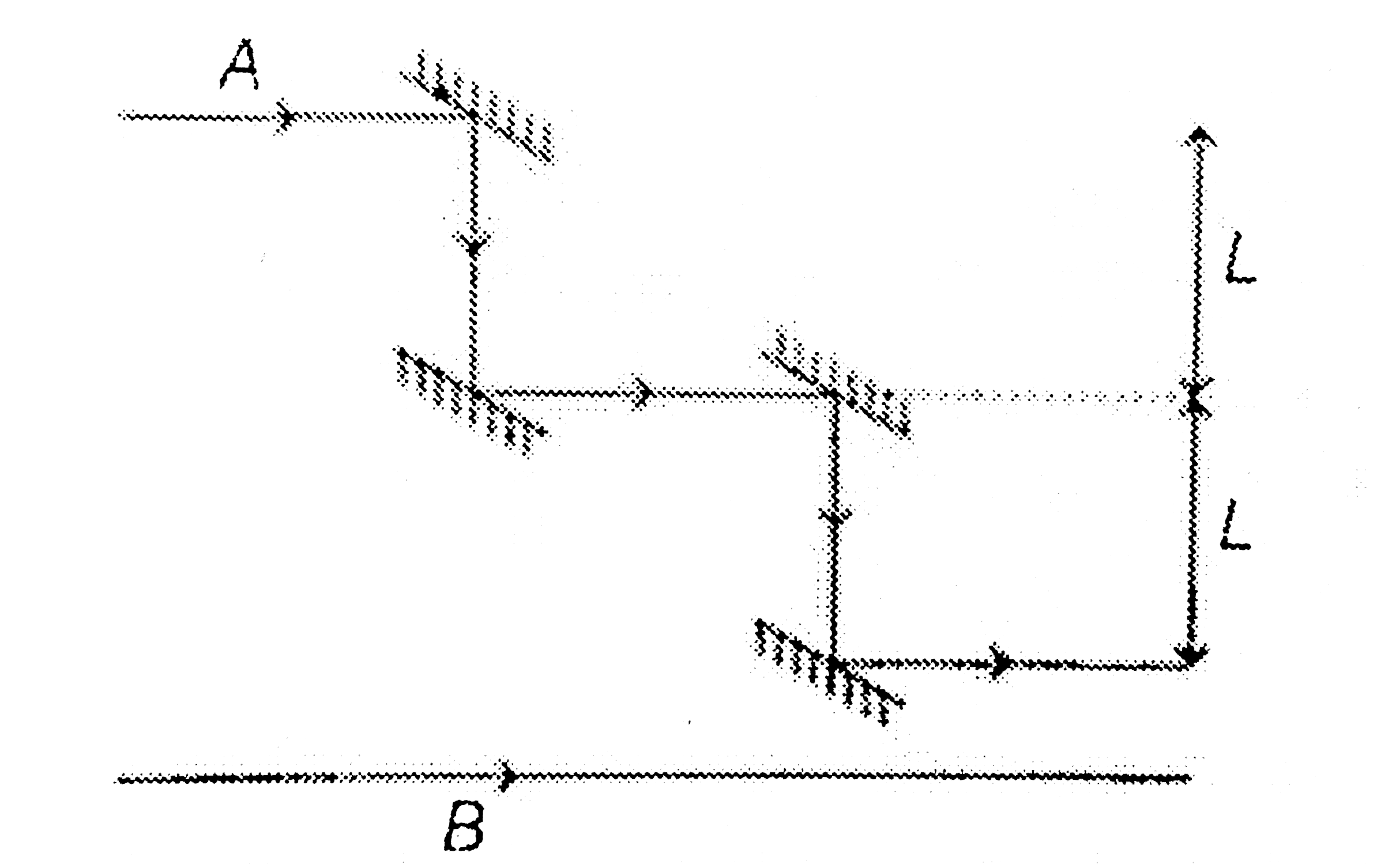
View SolutionIn the figure shown, light waves A and B both of wavelength λ are initially in phase and travelling rightward as incident by the two rays. Wave A is reflected from four parallel surfaces but ends up travelling in original direction. The possible value(s) of distance L in terms of wavelength λ in figure which put A and B exactly out of phase with each other after all the reflected is/are
View SolutionLight waves of wavelength 5460 A, emitted by two coherent sources, meet at a point after travelling different paths. The path difference between the two wave trains at that point is 2.1μm. then phase difference will be ?
View SolutionAn indian submarine is moving in the Arabian sea with constant velocity. To detect enemy it sends out sonar waves which travel with velocity 1050ms in water. Initially the waves are getting reflected from a fixed island and the reflected waves are coming back to submarine. The frequency of reflected waves are detected by the submarine and found to be 10% greater than the sent waves.
Now an enemy ship comes in front, due to which the frequency of reflected waves detected by submarine becomes 21% greater than the sent waves.
Q If the wavelength received by enemy ship is λ' and wavelength of reflected waves received by submarine is λ'', then (λ'λ'') equals

View SolutionIn a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5−m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
View Solution
